Question

Transcribed Image Text:Q1
V(x)
a: The figure to the right shows a potential well where V(X)=0 for 0<x<a and V(X)=V₁
everywhere else. We want to place an electron in this
well in its ground state (lowest energy eigenstate). What
can you say about the energy of this electron as the value,
V₁, increases?
A. The electron's energy will increase
B. The electron's energy will decrease
C. The electrons energy will remain the same
D. There is not enough information
E. It depends on the position where you measure the energy
b: Briefly explain your reasoning
0
V₁
a
Expert Solution
arrow_forward
Step 1: Determining the given data
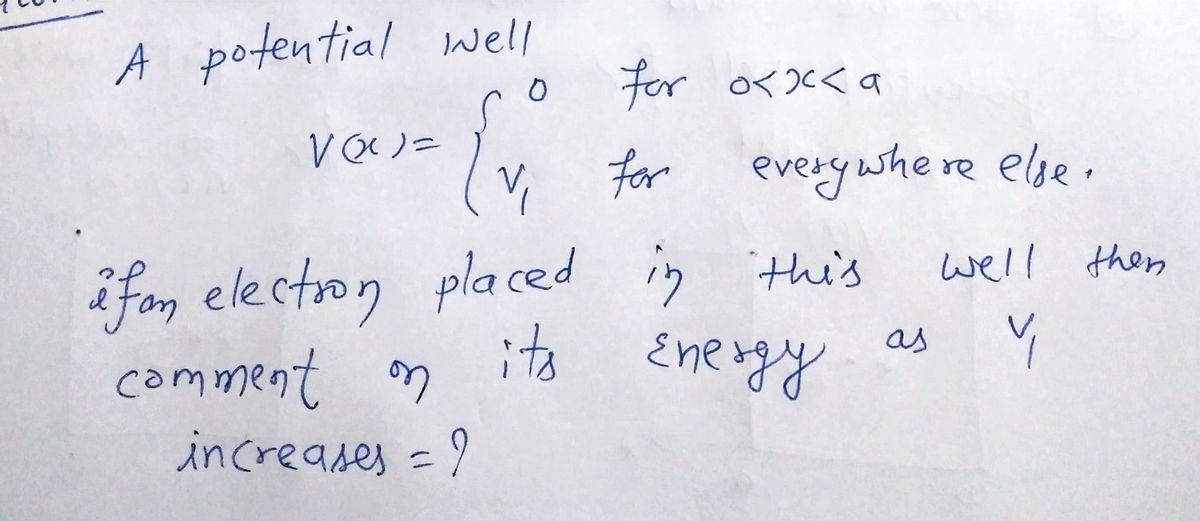
Step by stepSolved in 4 steps with 3 images

Knowledge Booster
Similar questions
- 6. In Dirac notation, after the equation Bø) = b|p)is solved, we often write the solutions as {|Øn)} and {bn}. The name given to {b,} is it is the spectrum of the operator B . Essentially problem 5 and problem 6 are describing identical situations. What is the relationship between pn (x) and |Øn)? To answer this, give a mathematical answer and a physical interpretation of what it means. Hint: If you do not know how to answer this off the top of your head as being obvious, review my notes on Dirac notation and how vectors are used in quantum mechanics.arrow_forwardQ1. Consider the finite square well potential shown in the following diagram: U(x) E>0 L The potential is given by: for xL| -U. for 0 0is incident on this region from the left. Using the plane A particle with energy wave approximation for the particle: a) Show that Y = Ae*+Be¬k* is a suitable general solution to the time-independent Schrödinger wave-equation (TISE) that applies in the region x L write down the four equations arising from the boundary conditions that apply at x=0 and x=L .arrow_forwardQ4. Show that the Legendre polynomials are orthogonal solutions of the angular part of the Schrodinger equation.arrow_forward
- The electron moves in an infinitely deep. potential well with a width of l=0.15 nm. a) Calculate the minimum (i.e. ground state) speed of the electron. V₁=? b) Calculate the reaction force that the electron causes when it moves back and forth and collides with the other wall of the well adiabatically (thermally insulated). F=? c) Calculate the frequency of the electron's back and forth motion. f=?arrow_forward0 A physical system is described by a two-dimensional vector space with Hamiltonian operator Ĥ given by Ĥ = (_) where a is a constant. At time t = 0, the system is prepared in state (t = 0)) = -i2.5 0 determine the expectation value (Ŝ) at time t = πħ/(4x). O a. 2.17 O b. -2.50 O c. -1.25 O d. 2.50 O e. 5.00 0 (¹). For operator $ = (2 i2.5arrow_forward
arrow_back_ios
arrow_forward_ios