
Elementary Linear Algebra (MindTap Course List)
8th Edition
ISBN: 9781305658004
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
I want a mathematical solution, not an explanation and definitions of a proof using one of the well-known methods
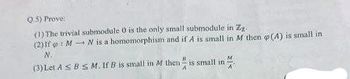
Transcribed Image Text:Q.5) Prove
(1) The trivial submodule 0 is the only small submodule in Zz
(2) If MN is a homomorphism and if A is small in M then (A) is small in
(3) Let ABS M. If B is small in M then
M
is small in
A
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 9 images

Knowledge Booster
Similar questions
- Find all monic irreducible polynomials of degree 2 over Z3.arrow_forwardProve that if a subring R of an integral domain D contains the unity element of D, then R is an integral domain. [Type here][Type here]arrow_forwardProve statement d of Theorem 3.9: If G is abelian, (xy)n=xnyn for all integers n.arrow_forward
- Consider the mapping :Z[ x ]Zk[ x ] defined by (a0+a1x++anxn)=[ a0 ]+[ a1 ]x++[ an ]xn, where [ ai ] denotes the congruence class of Zk that contains ai. Prove that is an epimorphism from Z[ x ] to Zk[ x ].arrow_forwardComplete the proof of Theorem 5.30 by providing the following statements, where and are arbitrary elements of and ordered integral domain. If and, then. One and only one of the following statements is true: . Theorem 5.30 Properties of Suppose that is an ordered integral domain. The relation has the following properties, whereand are arbitrary elements of. If then. If and then. If and then. One and only one of the following statements is true: .arrow_forwardLet be as described in the proof of Theorem. Give a specific example of a positive element of .arrow_forward
- For an element x of an ordered integral domain D, the absolute value | x | is defined by | x |={ xifx0xif0x Prove that | x |=| x | for all xD. Prove that | x |x| x | for all xD. Prove that | xy |=| x || y | for all x,yD. Prove that | x+y || x |+| y | for all x,yD. Prove that | | x || y | || xy | for all x,yD.arrow_forwardDescribe the kernel of epimorphism in Exercise 20. Consider the mapping :Z[ x ]Zk[ x ] defined by (a0+a1x++anxn)=[ a0 ]+[ a1 ]x++[ an ]xn, where [ ai ] denotes the congruence class of Zk that contains ai. Prove that is an epimorphism from Z[ x ] to Zk[ x ].arrow_forwardThe mapping : (Z6, +6) → (U4, ×4) on y vong ban ,0 is avouritaco at η TUOX svong bps Its euouston ai Intify ca dad ted STON n→ 3" (mod 4) (G.e) sach that yo is a homomorphism. (Here U4 = {1,3}.) (a) Write down the image of each element of Z6 under o.1 osT sula unel (b) Find Imo and Ker o. 140 1 = (512 jest, dous (II-) is aut (d) State a standard group that is isomorphic to the quotient group (c) Write down the cosets of Ker o in Z6- [8] ZG/Ker o. timil odi tadi orang of slu aham 8 - 0 58+arrow_forward
- 4. Let w = e 11, and let E = Q(w). (a) Verify that [E:Q] 10. (b) Determine |Gal(E/Q)|, the number of automorphisms of E that fix Q. (c) Find the order of y(w) w? in Gal(E/Q). (d) How many subfields K does E have (such that QC K C E)? Hint 1 The corollary to Eisenstein's theorem might help. Hint 2: Example 6, page 535 may help.arrow_forward6. Let R be an integral domain and M an R-module. Define TorR(M)= {me Mrm = 0, r/ 0} (a) Prove TorR(M) is a submodule of M (b) Form the quotient module M/TorR(M) (recall the module action is r. (m+ Torn(M)) = rm + TorR(M)). Prove TorR (R/Tor (M)) is zero (i.e., it equals {0+ TorR(M)}) Consider tharrow_forwardShow that (p(x), q(x)) = p(0)q(0) +p(1)q(1) +p(2)q(2) defines an inner product on P2.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning, Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning