Trigonometry (11th Edition)
11th Edition
ISBN: 9780134217437
Author: Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
I have solved one of the steps, how can I solve the rest? ALEKS wants to me to list each step and the rule.
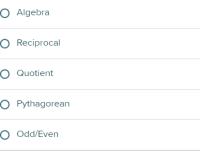
Transcribed Image Text:The image displays a multiple-choice selection list with five mathematics-related options. The options are as follows:
1. Algebra (Radio button: unselected)
2. Reciprocal (Radio button: unselected)
3. Quotient (Radio button: unselected)
4. Pythagorean (Radio button: unselected)
5. Odd/Even (Radio button: unselected)
![### Proving the Trigonometric Identity
#### Prove the identity:
\[ \sec^2{x} - \tan^2{x} = 1 \]
Note that each statement must be based on a Rule chosen from the Rule menu. To see a detailed description of a Rule, select the More Information Button to the right of the Rule.
---
#### Statements and Rules
| **Statement** | **Rule** |
|-----------------------------------|-----------|
| \(\sec^2{x} - \tan^2{x} = 1\) | Algebra |
To understand the proof of the given identity, let's break it down step-by-step using the fundamental trigonometric identities.
---
#### Detailed Explanation
##### Trigonometric Identities Used:
1. \(\sec{x} = \frac{1}{\cos{x}}\)
2. \(\tan{x} = \frac{\sin{x}}{\cos{x}}\)
3. Pythagorean Identity: \(\sin^2{x} + \cos^2{x} = 1\)
Given the identity to prove:
\[ \sec^2{x} - \tan^2{x} = 1 \]
By expressing \(\sec{x}\) and \(\tan{x}\) using their definitions in terms of sine and cosine:
\[ \sec^2{x} = \left(\frac{1}{\cos{x}}\right)^2 = \frac{1}{\cos^2{x}} \]
\[ \tan^2{x} = \left(\frac{\sin{x}}{\cos{x}}\right)^2 = \frac{\sin^2{x}}{\cos^2{x}} \]
Substitute these into the original equation:
\[ \frac{1}{\cos^2{x}} - \frac{\sin^2{x}}{\cos^2{x}} \]
Combine the fractions:
\[ \frac{1 - \sin^2{x}}{\cos^2{x}} \]
Using the Pythagorean identity:
\[ 1 - \sin^2{x} = \cos^2{x} \]
Substitute this back into the equation:
\[ \frac{\cos^2{x}}{\cos^2{x}} = 1 \]
Hence, the identity is proven:
\[ \sec^2{x} - \tan^2{x} = 1 \]
---
#### Interactive Diagram
To visualize how rules relate to different](https://content.bartleby.com/qna-images/question/38188fd7-32af-4cc1-9ec8-e56982db8708/7c5d9227-fea0-49ca-80b0-2536f727b685/4u0sgwl.png)
Transcribed Image Text:### Proving the Trigonometric Identity
#### Prove the identity:
\[ \sec^2{x} - \tan^2{x} = 1 \]
Note that each statement must be based on a Rule chosen from the Rule menu. To see a detailed description of a Rule, select the More Information Button to the right of the Rule.
---
#### Statements and Rules
| **Statement** | **Rule** |
|-----------------------------------|-----------|
| \(\sec^2{x} - \tan^2{x} = 1\) | Algebra |
To understand the proof of the given identity, let's break it down step-by-step using the fundamental trigonometric identities.
---
#### Detailed Explanation
##### Trigonometric Identities Used:
1. \(\sec{x} = \frac{1}{\cos{x}}\)
2. \(\tan{x} = \frac{\sin{x}}{\cos{x}}\)
3. Pythagorean Identity: \(\sin^2{x} + \cos^2{x} = 1\)
Given the identity to prove:
\[ \sec^2{x} - \tan^2{x} = 1 \]
By expressing \(\sec{x}\) and \(\tan{x}\) using their definitions in terms of sine and cosine:
\[ \sec^2{x} = \left(\frac{1}{\cos{x}}\right)^2 = \frac{1}{\cos^2{x}} \]
\[ \tan^2{x} = \left(\frac{\sin{x}}{\cos{x}}\right)^2 = \frac{\sin^2{x}}{\cos^2{x}} \]
Substitute these into the original equation:
\[ \frac{1}{\cos^2{x}} - \frac{\sin^2{x}}{\cos^2{x}} \]
Combine the fractions:
\[ \frac{1 - \sin^2{x}}{\cos^2{x}} \]
Using the Pythagorean identity:
\[ 1 - \sin^2{x} = \cos^2{x} \]
Substitute this back into the equation:
\[ \frac{\cos^2{x}}{\cos^2{x}} = 1 \]
Hence, the identity is proven:
\[ \sec^2{x} - \tan^2{x} = 1 \]
---
#### Interactive Diagram
To visualize how rules relate to different
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Similar questions
- if 4a+(7a)=65 what does a eqaularrow_forwardThe options for the first box are: step 1, 2, 3, or 4. The options for the second box are: a cube root cannot be a negative number, an integer raised to a negative number will not be less than one, the fraction should be added before multiplying by the cube root, and the square root of the sum does not equal the sum of the square roots. The options for the 3rd box are: -110, -75.2, 15.2, 20.8arrow_forwardYou need to fly from NYC to LA with a stopover in Dallas. If there are three different flights available from NYC to Dallas and four different flights available from Dallas to LA , now many different trips can you take?arrow_forward
Recommended textbooks for you
- Trigonometry (11th Edition)TrigonometryISBN:9780134217437Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie DanielsPublisher:PEARSON
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (11th Edition)
Trigonometry
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:PEARSON
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning