
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Pp# 1: can you help me solve and understand this practice problem please? A step by step explanation would be appreciated. Thank you!
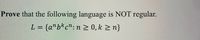
Transcribed Image Text:**Prove that the following language is NOT regular.**
\( L = \{ a^n b^k c^n : n \geq 0, k \geq n \} \)
---
**Explanation:**
This statement is asking to demonstrate that the language composed of strings with the form \(a^n b^k c^n\), where \(n\) is greater than or equal to 0, and \(k\) is greater than or equal to \(n\), cannot be represented by a regular expression or finite automaton. Regular languages are typically those that can be expressed with regular expressions or finite automata, and proving that a language is not regular often involves showing that these mechanisms are insufficient to capture its structure.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps

Knowledge Booster
Similar questions
- I am having trouble understanding the solution. Also the hints do not seem to be used. Some elaboration would be great, thanks!arrow_forwardCan you guide me to solve this problem? ''when a number is decreased by 20% the result is 136'' on TI-30XS Caculator, Homework: 6.3 Applications of Linear Equations CC2arrow_forwardCan you show equations and work to pleasearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

