Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: A(x + y) = Ax + Ay. 2. A(ax) = a(Ax) = (aA)x
A:
Q: If A ∈ R^n×n is invertible, then columns of A^−1 are linearly independent. Explain why.
A:
Q: If any three square matrices have the same size as A ,B,C AB=I and CA=I prove that A=C=A^-1
A:
Q: If A,B,C are nxn invertible matrices and I is nxn unit matrix C-(A + X)B¬1 = I What is the solution…
A: Given that C-1(A+X)B-1=I   To Find: X=?…
Q: Suppose A is a non-singular matrix. Using properties of the determinant, show that det(A^−1) =…
A:
Q: For A S calculate I+tA+ 0.904837 (-2-6) X 10 -0.200334 X 1.10517 t2 The actual value of e014, to six…
A:
Q: If matrix A, B and C are invertible matrix of same order then (ABC)^(-1) = * C^-1) x B^(-1) x A^(-1)…
A: Given that A,B and C are invertible matrices of the same order.
Q: Theorem 7.5.3. Let V be a finite-dimensional vector space over C and T € L(V,V). Then there erists a…
A: Note: Basis can't be compared with the image of (A - lambda*Identity). Given information: V = R2 and…
Q: Diaganolize the following matrix such that: D=(P^T)(A)(P). Rather than finding the inverse matrix,…
A:
Q: Which of the following subsets of the sets in the set of real square matrices of size 2 x 2 is…
A:
Q: The following matrix product is used in discussing two thin lenses in air: (1 -1/f2 M where fi and…
A:
Q: Create a 3x3 matrix A with a determinant of 10. Then, compute the matrix of cofactors of A and the…
A:
Q: 5. Prove that the cigenvalues of a Hermitian matrix are always real-valued, and that the inner…
A: Both the proofs of the given question has been proved in step 2 and step 3.
Q: te the above linear system (of one equation) as a homogeneous matrix problem.
A:
Q: for Find property 8. Give matrix A and constants c and d so that Cc+d) @ A# (COA) + (LOA) a…
A: To give a counterexample to property c+d⊗A≠c⊗A⊕d⊗A. Here A is a matrix and c, d are scalars. The…
Q: Please explain how the chracteristic polynomial = -(lambda - 3)(lambda - 3)(lambda - 2) for the…
A:
Q: For a non - singular square matrix 4, if A ^ 3 = A, then A must be (A) a nilpotent matrix (B) an…
A:
Q: matrix A and matrix B are defined in image calculate 3A-3B then find 6A^T
A:
Q: A,B square matrices A^3=B^3, A^2B=B^2A, A^2+B^2 invertible Show A=B
A: see below the answer
Q: "36. Prove that a square matrix A is invertible if and only if A^TA is invertible
A:
Question
An n x n matrix A is skew symmetric if A^(-1)=A^t. Prove that if A is invertible and skew-symmetric that A^(-1) is also skew symmetric (use the properties of inverses.) You need to show that (A^(-1))^t=-A^(-1) . Select the antecedent of the theorem you are proving, then prove the theorem in the box provided. If attaching a file, use only pdf format.
Expert Solution
Check Mark
Step 1

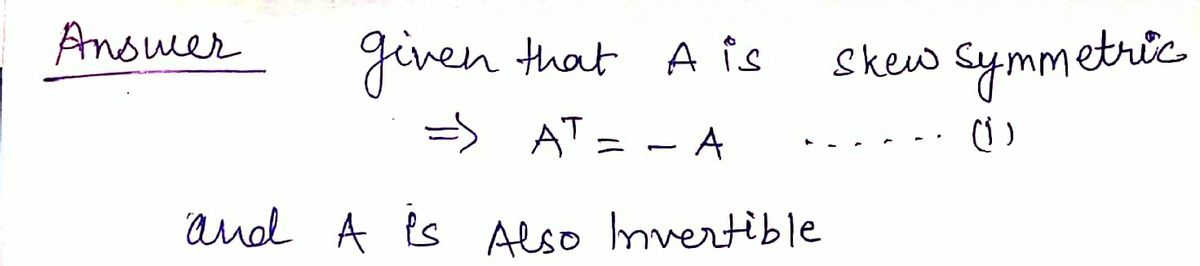
Advanced Math homework question answer, step 1, image 1

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS