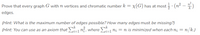
Prove that every graph G with n vertices and chromatic number k = x(G) has at most · (n2 – ) edges. (Hint: What is the maximum number of edges possible? How many edges must be missing?) (Hint: You can use as an axiom that =1 n%, where i=1 n¡ = n is minimized when each n; = n/k.)

4. Show that K6 is AY equivalent to the Petersen graph.

This is a discrete math (Trees) problem. Please explain each step in detail and do not copy solutions from Chegg.

Use the formula deg(v) = 2|E(G)| to find the number of edges of the following vЄV (G) graphs. Classify (count) the vertices by number of neighbors. (a) V(G) = [100]. Edges: for all n and m in [100], n ‡ m, n is adjacent to m if and only if |nm| ≤ 4. (b) V(G) = [10] × [10]. Edges: for all (a, b) and (c,d) in [10] × [10], (a, b) ‡ (c,d), (a, b) is adjacent to (c,d) if and only if a = c or b = d. (c) V(G) = [10] × [10]. Edges: for all (a, b) and (c,d) in [10] × [10], (a, b) ‡ (c,d), (a, b) is adjacent to (c,d) if and only if |ac| + |bd| = 1. (d) V (G) = [10] × [10]. Edges: for all (a, b) and (c,d) in [10] × [10], (a, b) is adjacent to (c,d) if and only if |a - c + b-d ≤ 2. (a, b) ‡ (c,d),