
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
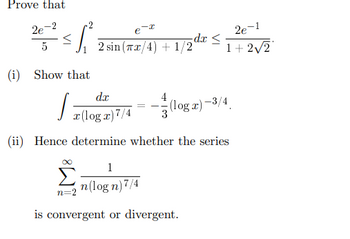
Transcribed Image Text:Prove that
2e
5
2 sin (Tx/4)+1/2
dx ≤
2e-1
1+2√2
(i) Show that
zloga 7/4
dx
-
(log)
(log x)-3/4
(ii) Hence determine whether the series
n=
1
n(logn) 7/4
is convergent or divergent.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 6 images

Knowledge Booster
Similar questions
- What is the limit as n goes to infinity of the power series (log n)2/nxn ?arrow_forwardVerify that Jp+1(x) + 2J½ (x) – Jp-1(x) = 0 Tip: Compare the series of Jp+1(x) – Jp-1(x) and – 2J½(x) = 0arrow_forward(2n+ 1)x Please explan Determine whether the series sin- converges or diverg es. If it converges, find its sum. thish L and how it nelotes to the n-D0 (4r + 1)x Since sin =1 and sin =-1 and the angle may be incremente by any multiple of 2x, then sin 2 =1 and (4r+3)a sin =-1, (any r). How does this nelate to the answer. Examine the partial sums of the series. The expanded series is sin 3n 5x + sin + sin ,+ sin + sin+ .. ansver Notice that the angles in consecutive even terms (n is even) differ by 2x, and the angles in consecutive odd terms (n is odd) differ by 2x. Since sin 0 = sin (0+2mx), all the even terms are equal to 1, and all the odd terms are equal to -1. Evaluating each term, the series is 1+(-1)+1+(-1)+1+ The partial sums altermate between 1 and 0, tending to (2n + 1)a neither value. Therefore, lim sin- k00 n=0 does not exist and the series diverges. detail. Pelease explain n thanke gou.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

