Prove that 2" < n! for all positive integers n such that n > 4.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
need this asap please show all the work and write out the prove step by step pleaseee
![**Mathematical Induction Problem:**
**Prove that**
\[ 2^n < n! \]
**for all positive integers \( n \) such that \( n \geq 4 \).**
### Explanation:
This mathematical statement asserts that for any integer \( n \) that is 4 or greater, the value of \( 2^n \) (two raised to the power of \( n \)) is less than \( n! \) (the factorial of \( n \)).
The proof typically involves using mathematical induction, a method of mathematical proof typically used to establish a given statement for all natural numbers.
### Steps of Proof:
1. **Base Case:** Verify the inequality for the initial value \( n = 4 \).
2. **Inductive Step:**
- Assume the statement holds for some integer \( k \geq 4 \). That is, assume \( 2^k < k! \).
- Prove that the inequality also holds for \( k+1 \), i.e., \( 2^{k+1} < (k+1)! \).
### Inductive Process:
To complete the proof, each of these steps would need to be verified. The base case typically requires plugging the initial value into both sides of the inequality. The inductive step involves algebraic manipulation and logical reasoning to show the inequality holds for \( k+1 \) based on the assumption that it holds for \( k \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fba208968-0ccc-4a94-8921-5ea260cefe19%2Fd0027565-9f46-4c97-aa01-a2eae17a7e90%2Fdbm0qhb_processed.png&w=3840&q=75)
Transcribed Image Text:**Mathematical Induction Problem:**
**Prove that**
\[ 2^n < n! \]
**for all positive integers \( n \) such that \( n \geq 4 \).**
### Explanation:
This mathematical statement asserts that for any integer \( n \) that is 4 or greater, the value of \( 2^n \) (two raised to the power of \( n \)) is less than \( n! \) (the factorial of \( n \)).
The proof typically involves using mathematical induction, a method of mathematical proof typically used to establish a given statement for all natural numbers.
### Steps of Proof:
1. **Base Case:** Verify the inequality for the initial value \( n = 4 \).
2. **Inductive Step:**
- Assume the statement holds for some integer \( k \geq 4 \). That is, assume \( 2^k < k! \).
- Prove that the inequality also holds for \( k+1 \), i.e., \( 2^{k+1} < (k+1)! \).
### Inductive Process:
To complete the proof, each of these steps would need to be verified. The base case typically requires plugging the initial value into both sides of the inequality. The inductive step involves algebraic manipulation and logical reasoning to show the inequality holds for \( k+1 \) based on the assumption that it holds for \( k \).
Expert Solution
Step 1
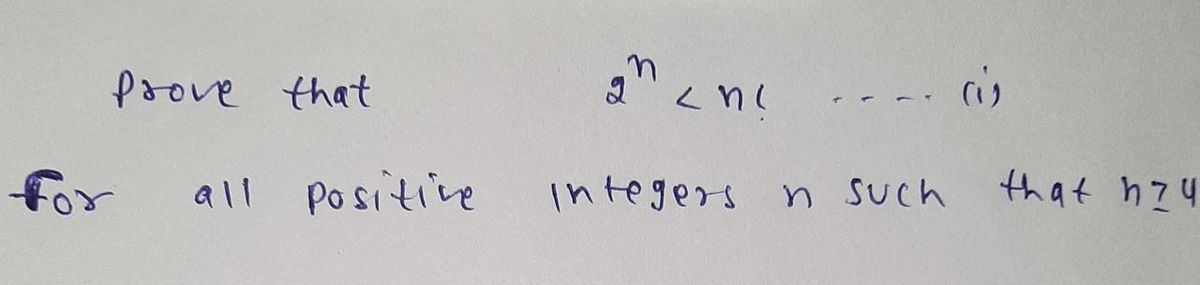
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

