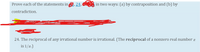
Prove each of the statements in , 24, G in two ways: (a) by contraposition and (b) by contradiction. 24. The reciprocal of any irrational number is irrational. (The reciprocal of a nonzero real number a is 1/æ.)

(24) We have to show that the reciprocal of any irrational number is irrational.

(a) Now, prove the given statement by contrapositive.

The contrapositive statement is "If $\frac{1}{x}$ is rational then $x$ is a rational, for $x\in R$, $x\ne 0$

Assume that $\frac{1}{x}$ is a rational number.

Clearly, $\frac{1}{x}$ is nonzero.

By the definition of rational number, $\frac{1}{x}=\frac{a}{b}$ for $a,b\in Z$, $a\ne 0,b\ne 0$

$\Rightarrow \frac{b}{a}=x$

Hence, by definition of rational, $x$ is a rational number.

Hence, proved.