
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question

Transcribed Image Text:Problem 9 You shine your favorite laser pointer (which has a wavelength of 450 nm) towards two slits a
distance d apart. You then observes the second order (m=2) bright fringe to be 5.0 cm away from the central
bright maximum on a screen 4.0 meters away. You now shine your second favorite laser pointer (which has
a wavelength of 530nm) onto the slits, how far away from the central bright maximum will the third order
(m=3) bright fringe be located?
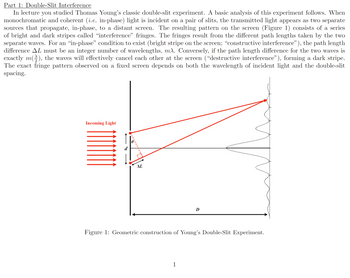
Transcribed Image Text:Part 1: Double-Slit Interference
In lecture you studied Thomas Young's classic double-slit experiment. A basic analysis of this experiment follows. When
monochromatic and coherent (i.e. in-phase) light is incident on a pair of slits, the transmitted light appears as two separate
sources that propagate, in-phase, to a distant screen. The resulting pattern on the screen (Figure 1) consists of a series
of bright and dark stripes called "interference" fringes. The fringes result from the different path lengths taken by the two
separate waves. For an “in-phase" condition to exist (bright stripe on the screen; "constructive interference"), the path length
difference AL must be an integer number of wavelengths, mλ. Conversely, if the path length difference for the two waves is
exactly m(), the waves will effectively cancel each other at the screen ("destructive interference"), forming a dark stripe.
The exact fringe pattern observed on a fixed screen depends on both the wavelength of incident light and the double-slit
spacing.
Incoming Light
AL
D
Figure 1: Geometric construction of Young's Double-Slit Experiment.
1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Monochromatic light of wavelength 650 nm is incident normally on a diffraction grating. If the second-order maximum of the diffraction pattern is observed at 22° from the centerline, what is the distance between the slits of the grating? O 3.5 um 0 1.4 km 2.8 μm O 8.5 kmarrow_forwardA beam from a krypton ion laser (gamma = 461.9 nm) falls on a single slit, producing a central maximum 4.0cm wide on a screen 1.50m away. a. Calculate the slit width b. Determine the angle between the rays travelling to the 2nd minima and the rays travelling to the central maxima.arrow_forwardK:18)arrow_forward
- A laser beam is normally incident on a single slit with width 0.620 mm. A diffraction pattern forms on a screen a distance 1.35 m beyond the slit. The distance between the positions of zero intensity on both sides of the central maximum is 2.18 mm. Calculate the wavelength of the light (in nm). nm Need Help? Read Itarrow_forwardWhen illuminating the observation screen directly, without any slits, you notice that the laser has a spread, meaning that the light on the screen becomes larger as you increase the distance between you and the screen. Determine the angular spread of the 710.5 nm wavelength laser beam if the circular aperture of the laser is 0.7 mm in diameter. Enter your answer in milli-rad with 2 decimal place precisionarrow_forwardLight with wavelength i passes through a narrow slit of width w and is seen on a screen which is located at a distance D in front of the slit. The first minimum of the diffraction pattern is at distance d from the middle of the central maximum. Calculate the wavelength of light if D=3.1 m, d=1 mm and w = VAD. Give your answer in nanometers. Answer: nm Next pagearrow_forward
- beam of monochromatic light is incident on a single slit of width 0.560 mm. A diffraction pattern forms on a wall 1.20 m beyond the slit. The distance between the positions of zero intensity on both sides of the central maximum is 2.36 mm. Calculate the wavelength of the light. nm A helium-neon laser (A = 632.8 nm) is used to calibrate a diffraction grating. If the first-order maximum occurs at 20.1 Degree , what is the spacing between adjacent grooves in the grating? (In this problem, assume that the light is incident normally on the gratings.) pm White light is spread out into its spectral components by a diffraction grating. If the grating has 1 980 grooves per centimeter, at what angle does red light of wavelength 640 nm appear in first order? (Assume that the light is incident normally on the gratings.)arrow_forwardYou perform a double-slit experiment in order to measure the wavelength of the new laser that you received for your birthday. You set your slit spacing at 1.05 mm and place your screen 8.51 m from the slits. Then, you illuminate the slits with your new toy and find on the screen that the tenth bright fringe is 4.63 cm away from the central bright fringe (counted as the zeroth bright fringe). What is your laser's wavelength i expressed in nanometers? = nmarrow_forwardYou measure three segments of the distance between a diffraction slit an the screen on which the pattern forms: x1 = (15.8 ± 0.2) cm, x2 = (6.7 ± 0.1) cm, and x3 = (11.3 ± 0.1). What is the uncertainty of the total distance x1 + x2 + x3? Group of answer choices 0.4 cm 0.5 cm 0.2 cm 0.3 cm 0.1 cmarrow_forward
- A flat observation screen is placed at a distance of 4.7 m from a pair of slits. The separation on the screen between the central bright fringe and the first-order bright fringe is 0.035 m. The light illuminating the slits has a wavelength of 495 nm. Determine the slit separation. Number i Unitsarrow_forwardA nearly monochromatic beam of light with an average wavelength of 516 nm is incident normally on a diffraction grating 2.90 cm wide with 1300 lines/cm. What is the smallest wavelength difference (in nm) this grating can resolve in the second order diffraction with this beam?Type your answer herearrow_forwardPlease asaparrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON