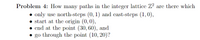
Problem 4: How many paths in the integer lattice Z? are there which • only use north-steps (0, 1) and cast-steps (1,0), start at the origin (0,0), • end at the point (30, 60), and • go through the point (10, 20)?

Suppose we used our failing perfect shuffling of digits to mix the digits of the numbers (x,y) that describe a point on the square to get a one-to-one correspondence with the points on a line segment. What point in the square would be paired with the point 0.12000100010001000100010001...?

3. The fractal C is constructed as follows. (i) Begin with the line segment Io = [0,1]. (ii) Remove the open middle third (}, }), to get I = [0, ] U [G, 1). (iii) Remove the open middle third from every remaining line segment, to get [2 1] I2 = [0, (iv) Repeat the process of removing the open middle thirds of the remaining line segments infinitely many times. The first few iterations of this construction are illustrated below. (a) Find the total length of the intervals removed from [0, 1] after three iterations, i.e. the total length of the intervals removed from [0, 1] to get Iz. (b) By considering a suitable series, show that the total length of all of the intervals removed is equal to 1. (c) Despite the fact that an infinite number of intervals of total length 1 have been removed to construct C, there are points in the interval [0, 1] that will never be removed, i.e. there are points in C. What is one such point?

Assume there are 3 ways to get from point A to B and 5 ways to get from B to C. How many possible ways are there to get from A to C through the path of B?