
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
thumb_up100%
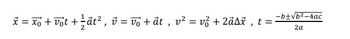
Transcribed Image Text:x = xót vót tật, ở = To +ất, v = vỏ +2āA,t=i
+
-b+√b²-4ac
2a

Transcribed Image Text:Problem 4:
A catapult launches a test rocket vertically upwards from a well, giving the rocket an initial
speed of 80 m/sec at ground level. The engines then fire, and the rocket accelerates upward at
4 m/sec² until it reaches an altitude of 1000 m.
a) How long does it take the rocket to reach the altitude of 1000 m? Answer: 10 sec
b) What is the speed of the rocket when it reaches an altitude of 1000 m? Answer: 120
m/sec
AY
Time t
y = 1000 m-
t=0
Yo
0.
Vo = 80 m/sec
a = 4 m/sec²
18
When the rocket reaches an altitude of 1000 m, the engines fail and the rocket goes into free
fall, with an acceleration of a = -g. For the remainder of this problem, the rocket engines will
be off. We will re-define t = 0 sec to be the time when the rocket is at an altitude of 1000 m.
The initial properties of the rocket will be the properties of the rocket at 1000.
v = 0 m/sec
Ymax
Engines On
c) What is the largest height the rocket reaches? Answer: 1734.7 m
d) What is the time it takes the rocket to hit the ground? Answer: 31.06 sec
e) What is the velocity of the rocket just before it hits the ground? Answer: -184.4 m/sec
AY
Redefine as t = 0
Yo = 1000 m
Vo = 120 m/sec
d=-g
g = 9.8 m/sec²
Engines Off
Įä
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The drawing shows a skateboarder moving at 6.80 m/s along a horizontal section of a track that is slanted upward by 0 = 41.0° above the horizontal at its end, which is 0.780 m above the ground. When she leaves the track, she follows the characteristic path of projectile motion. Ignoring friction and air resistance, find the maximum height H to which she rises above the end of the track. 6.80m/s 0.780marrow_forwardA bowling ball is attached to a 3.73-meter long cable and hung from the ceiling. The cable is kept taut and the ball is raised to an initial height of 1.73 meters above the classroom floor. It is released from rest and allowed to swing as a pendulum. Determine its speed (in m/s) when it is at a height of 1.19 meters above the floor. Answer: m/s (round to the nearest hundredth)arrow_forwardWe drop a plastic ball to the floor from a height of 2.0 m and let it bounce several times. 30% of energy is lost with each bounce. How much time passes between the first and second bounce and between the second and third bounce?arrow_forward
- A 0.25 kg mass is placed on a vertically oriented spring that is stretched 0.56 meters from its equilibrium position. If the spring constant is 105 N/m, how fast will the mass be moving when it reaches the equilibrium position? Hint: You cannot ignore the change in gravitational potential energy in this problem. Please give you’re answer in m/s.arrow_forwardPlease answer the question correctly. Thank you!!arrow_forwardYou cast a pebble at 2.4 m/s at a pond from 0.8 m above ground. How fast is it when it is about to land in the pond .5 m below the ground? Hint: use mechanical energy conservation. The direction of the velocity is irrelevant. It doesn't have to travel straight up or down. Pebble's final position is negative.arrow_forward
- A ball of mass 0.5kg is tied to a string of length 1.0 meters, and the other end of the string is tied to a rigid support. The ball is held straight out horizontally and is then released. a) What is the speed of the ball at the lowest point of its motion? b) What is the tension in the string at its joint? Solution FBD and Formula Requiredarrow_forwardThe drawing shows a skateboarder moving at 6.70 m/s along a horizontal section of a track that is slanted upward by 0 = 48.0° above the horizontal at its end, which is 0.530 m above the ground. When she leaves the track, she follows the characteristic path of projectile motion. Ignoring friction and air resistance, find the maximum height H to which she rises above the end of the track. 6.70m/s 0.530marrow_forwardThe rate of energy use in a typical house is about 2 kW. If the kinetic energy of a car (mass 1358 kg) is equal to the total energy used by the house in 1 min, what is the car's speed? m/sarrow_forward
- A man on a motorcycle plans to make a jump as shown in the figure. If he leaves the ramp with a speed of 28.5 m/s and has a speed of 26.2 m/s at the top of his trajectory, determine his maximum height (h) (in m) above the end of the ramp. Ignore friction and air resistance.arrow_forwardThe skateboarder in the drawing starts down the left side of the ramp with an initial speed of 5.0 m/s. Neglect nonconservative forces, such as friction and air resistance, and find the height h of the highest point reached by the skateboarder on the right side of the ramp. + 2.5arrow_forwardA skier, starting from rest, moves from the top of a ramp to the bottom. If the vertical drop is 3.12 meters, what is the speed in m/s of the skateboarder at the bottom of the ramp. (neglect friction). Can you help with a visual aid; and then, explain the mechanics of calculation.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON