
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
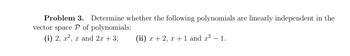
Transcribed Image Text:Problem 3. Determine whether the following polynomials are linearly independent in the
vector space P of polynomials:
(i) 2, x², x and 2x + 3;
(ii) x + 2, x + 1 and 2² 1.
Expert Solution
arrow_forward
Step 1
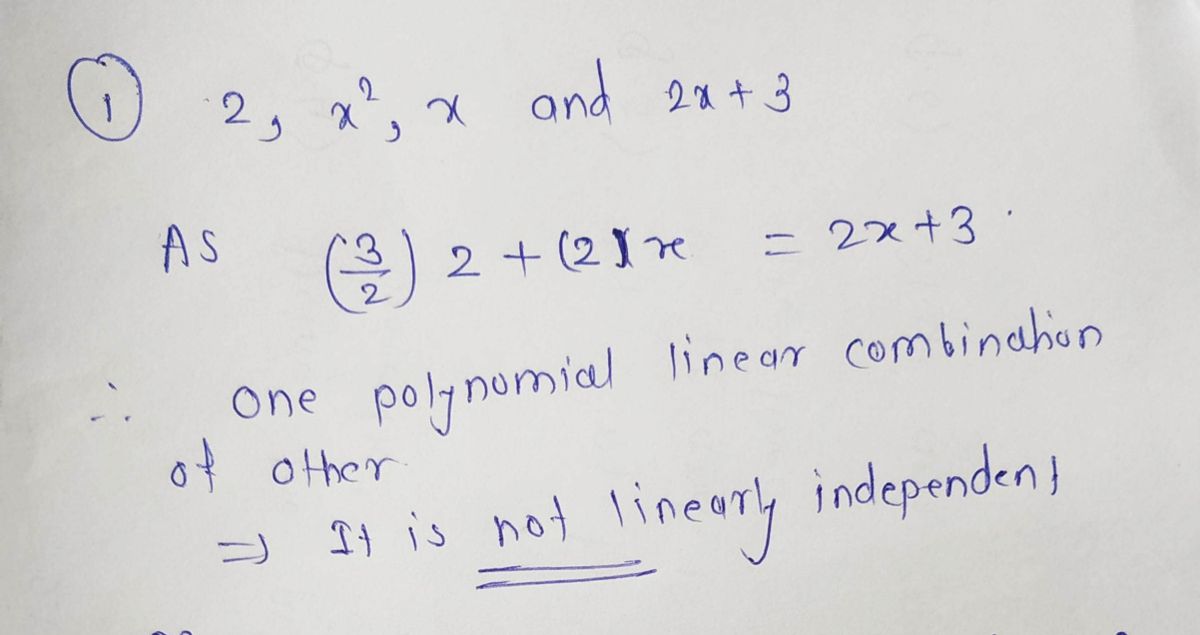
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- How would I find the basis and range rank for this linear algebra question?arrow_forward2x2 – 3x – 6, Question 2. Are the polynomials x2 – 2x +1, a) Linearly independent? -x2 + 5x – 3, 3x2 + 8x – 6 € P2: YES - NOarrow_forwardThis is a question from a linear algebra course: Let V = R[X]3, the polynomials of degree at most three, and B = {1, X, X2, X3}. Show what the image under fB is of:• the four basic elements: P1(X) = 1, P2(X) = X, P3(X) = X2 and P4(X) = X3• P(X) = 2 + 6X + 3X2 + 4X3arrow_forward
- 3: Which of the following sets are closed under scalar multiplication? (1) The set of all vectors in R of the form (a, b, 9ab). (i1) The set of all polynomials a- bx+ cx in P, such that ac =D0. (iii) The set of all matrices in Mn such that A = A (A) (1) and (ii) only (B) (1) and (iii) only (C) (ii) and (iii) only (D) (1) only (E) (ii) only (F) none of them (G) (iii) only (H) all of themarrow_forward1. Determine whether the following polynomials span P. =1+x, p, = 1 – x, P2 P3D1+x+x², P, = 2-x² 3D2 3:28 PM 豆 IA 2/23/2022 e Type here to search WQHD | 165HZ NOG ZEPHYRUS 100% DC-P3 PANTONE Validated F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 ESC E3 O/京 DELETE AURA 23 24 4 @ % & 7 { } TAB Q W E T Y P. [ 1O 15 林arrow_forwardPlease answer A, B, and C in question #1.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

