
Practical Management Science
6th Edition
ISBN: 9781337406659
Author: WINSTON, Wayne L.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:**Table 18.4: Infinite-Source Values for \( L_q \) and \( P_0 \) Given \( \lambda/\mu \) and \( M \)**
This table provides the infinite-source queueing values for \( L_q \) (average number of customers in line) and \( P_0 \) (probability of zero customers in the system) based on the ratio \( \lambda/\mu \) (arrival rate/service rate) and the number of servers \( M \).
Each row of the table is organized as follows:
- **\( \lambda/\mu \)**: This column lists the ratio of arrival rate to service rate, ranging from 0.15 to 4.3.
- **\( M \)**: Indicates the number of servers in the system, ranging from 1 to 10.
- **\( L_q \)**: Represents the average number of customers in line for the queue.
- **\( P_0 \)**: Shows the probability that there are zero customers in the system.
For each value of \( \lambda/\mu \), data is arranged under different values of \( M \), showing how \( L_q \) and \( P_0 \) vary with changes in these parameters.
The table helps in understanding how queue lengths and idle probabilities fluctuate with different server counts and demand ratios, facilitating decision-making in service systems planning and optimization.
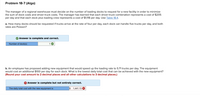
Transcribed Image Text:**Problem 18-7 (Algo)**
The manager of a regional warehouse must decide on the number of loading docks to request for a new facility in order to minimize the sum of dock costs and driver-truck costs. The manager has learned that each driver-truck combination represents a cost of $205 per day and that each dock plus loading crew represents a cost of $1,118 per day. Use Table 18.4.
**a. How many docks should be requested if trucks arrive at the rate of four per day, each dock can handle five trucks per day, and both rates are Poisson?**
- **Answer is complete and correct.**
- Number of dock(s): **1**
**b. An employee has proposed adding new equipment that would speed up the loading rate to 5.71 trucks per day. The equipment would cost an additional $100 per day for each dock. What is the lowest daily total cost that can be achieved with the new equipment? (Round your cost amount to 2 decimal places and all other calculations to 3 decimal places.)**
- **Answer is complete but not entirely correct.**
- The daily total cost with the new equipment is: **$1,441.13**
*Explanations:*
- Part (a) Analysis: The number of docks is calculated based on the arrival rate and handling capacity, ensuring the optimal number of docks to minimize costs.
- Part (b) Analysis: An additional cost is considered with new equipment. The proposed loading rate adjustment and its financial impact on daily costs are evaluated. The given answer may need reassessment for full accuracy.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- Ee 264.arrow_forwardSTOOGE ENTERPRISES Stooge Enterprises (Stooges) manufactures wooden mallets for commercial and residential applications. Stooges landed a major contract as a supplier to Slapsticks, Inc., a leading retailer in several major cities throughout the upper Midwest. Because of the large volume of demand, Stooges has to expand its manufacturing operation to three shifts and hire additional workers. Not long after Stooges began mallets to Slapsticks, it began receiving some complaints about mallet head diameters. This problem was somewhat alarming to Stooges, because its reputation as a high-quality manufacturer was the principal reason that it was selected as a supplier to Slapsticks. Stooges placed a great deal of confidence in its manufacturing capability because of its well trained and dedicated employees, and it never felt the need to consider formal process control approaches. In view of the recent complaints, the company president suspected that the expansion to a three-shift…arrow_forwardExactly what does it imply when we talk about "Infrastructure as a Service?"arrow_forward
- Give one example of linear bus bay in Chicagoarrow_forwardPls solve this question correctly in 5 min i will give u like Question # 2 A company produces two products, A and B. The sales volume for product A is at least 40% of the total sales of the two products. Both products use the same raw material, of which the daily availability is limited to 200 kg. Products A and B use this raw material at the rates of 5 kg/unit and 2 kg/unit, respectively. The sales prices for the two products are $50 and $20 per unit. Determine the following: a)Optimum volume of each product to be produced? b)What impact does the production mix have, in case the sales price of Product B decreases by 50%?arrow_forwardCan you explain what a laptop docking station is and how it functions?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage, Operations ManagementOperations ManagementISBN:9781259667473Author:William J StevensonPublisher:McGraw-Hill Education
Operations ManagementOperations ManagementISBN:9781259667473Author:William J StevensonPublisher:McGraw-Hill Education Operations and Supply Chain Management (Mcgraw-hi...Operations ManagementISBN:9781259666100Author:F. Robert Jacobs, Richard B ChasePublisher:McGraw-Hill Education
Operations and Supply Chain Management (Mcgraw-hi...Operations ManagementISBN:9781259666100Author:F. Robert Jacobs, Richard B ChasePublisher:McGraw-Hill Education
 Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning Production and Operations Analysis, Seventh Editi...Operations ManagementISBN:9781478623069Author:Steven Nahmias, Tava Lennon OlsenPublisher:Waveland Press, Inc.
Production and Operations Analysis, Seventh Editi...Operations ManagementISBN:9781478623069Author:Steven Nahmias, Tava Lennon OlsenPublisher:Waveland Press, Inc.

Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,

Operations Management
Operations Management
ISBN:9781259667473
Author:William J Stevenson
Publisher:McGraw-Hill Education

Operations and Supply Chain Management (Mcgraw-hi...
Operations Management
ISBN:9781259666100
Author:F. Robert Jacobs, Richard B Chase
Publisher:McGraw-Hill Education


Purchasing and Supply Chain Management
Operations Management
ISBN:9781285869681
Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. Patterson
Publisher:Cengage Learning

Production and Operations Analysis, Seventh Editi...
Operations Management
ISBN:9781478623069
Author:Steven Nahmias, Tava Lennon Olsen
Publisher:Waveland Press, Inc.