
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
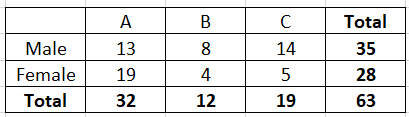
![**Probability of Selecting a Male Student or a Student with an "A" Grade**
In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution:
| | A | B | C | Total |
|--------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| Total | 32 | 12 | 19 | 63 |
**Objective:**
Determine the probability that a randomly selected student is either male or has received an "A" grade.
To solve this, we need to calculate:
1. Total students who are male.
2. Total students who received an "A".
3. Use the formula for probability with "or" condition:
\[
P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A})
\]
- **Total students**: 63
- **Total males**: 35
- **Total students with an "A"**: 32
- **Males with an "A"**: 13
Using the formula:
\[
P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857
\]
**Conclusion:**
The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.](https://content.bartleby.com/qna-images/question/71586c71-e002-40ed-a348-3617b1ab0846/a98ea1a7-db71-4b69-bc35-88041acf397e/xen1e6d.jpeg)
Transcribed Image Text:**Probability of Selecting a Male Student or a Student with an "A" Grade**
In this probability exercise, we analyze a group of students based on their grades and gender. The following table summarizes the distribution:
| | A | B | C | Total |
|--------|----|----|----|-------|
| Male | 13 | 8 | 14 | 35 |
| Female | 19 | 4 | 5 | 28 |
| Total | 32 | 12 | 19 | 63 |
**Objective:**
Determine the probability that a randomly selected student is either male or has received an "A" grade.
To solve this, we need to calculate:
1. Total students who are male.
2. Total students who received an "A".
3. Use the formula for probability with "or" condition:
\[
P(\text{Male or A}) = P(\text{Male}) + P(\text{A}) - P(\text{Male and A})
\]
- **Total students**: 63
- **Total males**: 35
- **Total students with an "A"**: 32
- **Males with an "A"**: 13
Using the formula:
\[
P(\text{Male or A}) = \frac{35}{63} + \frac{32}{63} - \frac{13}{63} = \frac{54}{63} = \frac{18}{21} \approx 0.857
\]
**Conclusion:**
The probability that a randomly selected student is either male or received an "A" is approximately 0.857, or 85.7%.
Expert Solution
arrow_forward
Step 1
Given information-
We have given the grades and gender of a group of students.
We have to find the probability that the student was male OR got an "A".
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- John runs a computer software store. He counted 120 people who walked by his store in aday, 50 of whom came into the store. Of the 50, only 21 bought something in the store.Estimate the probability that a person who walks by the store will come in and buysomething. Round your answer to the nearest hundredth. Group of answer choices 0.18 0.42 0.12 0.59 none of these choicesarrow_forwardThank you!arrow_forwardA quick quiz consists of a true/false question followed by a multiple-choice question with 6 possible answers. If both questions are answered with random guesses, find the probability that both responses are correct. Report the answer as a percent rounded to two decimal place accuracy. You need not enter the "%" symbol. Probability =arrow_forward
- rning utoring ← Q 72 this assessment. Clearly number each problem. Box all ansv the course. Giving a test to a group of students, the grades and ages are summarized below 7 Under 25 25 or older Total O 25 76 8 25 If one student is chosen at random, Find the probability that the student got a C. 8 76 Check Answer A B 16 9 8 15 11 17 31 20 25 #3 Question Help: Message instructor C C ANT $ 4 C E W Total 33 43 76 R Search or type URL LL F % LO 5 T MacBook Pro < 6 I work in a binder until the e G Y & 7 H ☆ U 8 + Jarrow_forwardFind the probability of selecting a red card from a standard deck of cards. a 1 4 1 52 1 2 d. 13arrow_forwardA high school baseball player has a 0.221 batting average. In one game, he gets 6 at bats. What is the probability he will get at least 2 hits in the game? Round your answer to four places. Submit Questionarrow_forward
- A pie chart reflects student performance... 16% As, 24% Bs, 32% Cs, 16% Ds, 12% Fs A. There were 317 students in total. How many students received As? B. If a student is selected at random what's the percentage it be a C student?arrow_forwardJohn runs a computer software store. He counted 124 people who walked by his store in a day, 52 of whom came into the store. Of the 52, only 21 bought something in the store. Estimate the probability that a person who walks by the store will enter the store. Round your answer to the nearest hundredth. Group of answer choices 0.59 0.25 0.42 0.17 none of these choicesarrow_forwardA couple has 3 kids. Use a tree diagram to find the probability thất they nàu irst gin. 8. 2. 3 8. 4.arrow_forward
- need help pleasearrow_forwardA group of people were asked if statistics teachers know the true meaning of life. 255 responded "yes", and 497 responded "no". Find the probability that if a person is chosen at random, he believes statistics teachers know the true meaning of life. Probability (Please enter a reduced fraction.) %Darrow_forwardSolve the attached file and selet the correct answer. Thanksarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
