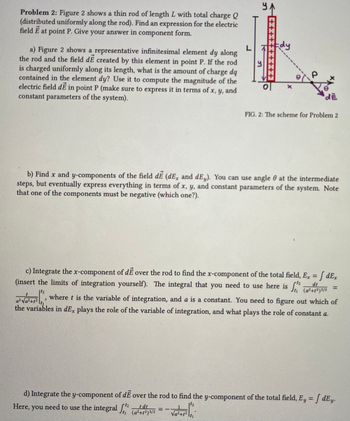
Problem 2: Figure 2 shows a thin rod of length L with total charge Q (distributed uniformly along the rod). Find an expression for the electric field E at point P. Give your answer in component form. a) Figure 2 shows a representative infinitesimal element dy along the rod and the field dE created by this element in point P. If the rod is charged uniformly along its length, what is the amount of charge dq contained in the element dy? Use it to compute the magnitude of the electric field dĒ in point P (make sure to express it in terms of x, y, and constant parameters of the system). L ул LC ▸ IV Edy P de FIG. 2: The scheme for Problem 2 b) Find x and y-components of the field dE (dEx and dEy). You can use angle at the intermediate steps, but eventually express everything in terms of x, y, and constant parameters of the system. Note that one of the components must be negative (which one?). c) Integrate the x-component of de over the rod to find the x-component of the total field, Ex = (insert the limits of integration yourself). The integral that you need to use here is ² dt fdEx (a²+1²)3/2 = ²√²+ where t is the variable of integration, and a is a constant. You need to figure out which of the variables in dEx plays the role of the variable of integration, and what plays the role of constant a. d) Integrate the y-component of de over the rod to find the y-component of the total field, Ey = | dEy. Here, you need to use the integral (41) 3/2

Next, imagine that a bullet impacts the block that you see and embeds itself. Let's say that you know the speed of the bullet just before it hits and also the mass of the bullet. Explain, with words and equations, how you would determine the angle theta. eed to know i L-h L Center of Pendulum catch

Please look at the picture to answer the question correctly.  Part 1) Which of the following represents a Newton's 2nd Law equation in the x direction?           a. Fnet,x = Ffs - Fw cos θ           b. Fnet,x = Ffs - Fw sin θ          c. Fnet,x = -Fw sin θ - Ffs          d. Fnet,x = Fn - Fw cos θ Part 2) Which of the following represents a Newton's 2nd Law equation in the y direction?          a. Fnet,y = Fw - Fn         b. Fnet,y = Fn - Fw sin θ         c. Fnet,y = Fw sin θ - Ffs         d. Fnet,y = Fn - Fw cos θ Please answer both parts

45 Please use energy to solve Please label all free body diagrams and any formulas used Thanks!