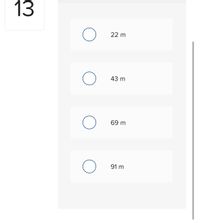
The image displays a multiple-choice question interface, numbered "13" on the left side. There are four answer options presented in a vertical list, each with a circular radio button to the left for selecting an option. The options are as follows: - Option 1: 22 m - Option 2: 43 m - Option 3: 69 m - Option 4: 91 m The interface is designed to allow users to select one of the options by clicking the corresponding radio button. ### Physics Problem: Projectile Motion #### Problem Statement A stone is thrown horizontally from a cliff with an initial speed of 10 m/s. It takes 4.3 seconds to hit the bottom of the cliff. Calculate the height of the cliff. #### Solution To find the height of the cliff, we can use the formula for the vertical motion of the stone. Since the stone is thrown horizontally, its initial vertical speed is 0 m/s. The vertical distance (height of the cliff) can be calculated using the formula for free fall: \[ h = \frac{1}{2}gt^2 \] Where: - \( h \) is the height, - \( g \) is the acceleration due to gravity (approximately \( 9.8 \, \text{m/s}^2 \) on Earth), - \( t \) is the time in seconds. Given: - \( t = 4.3 \, \text{s} \) Plugging in the values: \[ h = \frac{1}{2} \times 9.8 \times (4.3)^2 \] Calculate \( h \) to find the height of the cliff.

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.