
Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Question
Help!!! Please answer all Correctly!!! Please
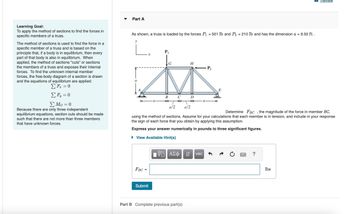
Transcribed Image Text:Part A
Review
Learning Goal:
To apply the method of sections to find the forces in
specific members of a truss.
The method of sections is used to find the force in a
specific member of a truss and is based on the
principle that, if a body is in equilibrium, then every
part of that body is also in equilibrium. When
applied, the method of sections "cuts" or sections
the members of a truss and exposes their internal
forces. To find the unknown internal member
forces, the free-body diagram of a section is drawn
and the equations of equilibrium are applied:
ΣΕ = 0
Σ Ε = 0
Στο = 0
Because there are only three independent
equilibrium equations, section cuts should be made
such that there are not more than three members
that have unknown forces.
As shown, a truss is loaded by the forces P₁ = 501 lb and P2 = 210 lb and has the dimension a = 9.50 ft.
P₁
B
T
a/2
C
*
a/2
H
-P₂
E
Determine FBC, the magnitude of the force in member BC,
using the method of sections. Assume for your calculations that each member is in tension, and include in your response
the sign of each force that you obtain by applying this assumption.
Express your answer numerically in pounds to three significant figures.
▸ View Available Hint(s)
1 ΑΣΦ Η vec
FBC =
Submit
Part B Complete previous part(s)
?
lbs
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- ! Required information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. At an intersection car B was traveling south and car A was traveling 30° north of east when they slammed into each other. Upon investigation, it was found that after the crash, the two cars got stuck and skidded off at an angle of 10° north of east. Each driver claimed that he was going at the speed limit of 50 km/h and that he tried to slow down, but couldn't avoid the crash because the other driver was going a lot faster. The masses of cars A and B were 1500 kg and 1200 kg, respectively. 10° 30° VR Determine the speed of the faster of the two cars if the slower car was traveling at the speed limit. The speed of the faster car was km/h.arrow_forwardAn exponent, such as the 4 in the expression 94, means: the number of times the number before the exponent is multiplied by itself (9 x 9 x 9x 9). O the number of times the number before the exponent is multiplied by 10 (9 x 10 x 10x 10 x 10). O the number to multiply the first number by (9 x 4). O the number of times the digit is written (9999). the number lo add to the first number (9 +4).arrow_forwardHello, so i have attached two images. the first image is the quetions, i need part b) answered if possible. i have attached my findings to part a) to add to the little information we know to help with part b if needed. Thnksarrow_forward
- Don't Use Chat GPT Will Upvotearrow_forwardI am attaching both questions for 4 and 5 with the question in the image. thank you. NOTE : So the last person answered this question WITHOUT refencing the answer for whether question 4 or 5 answeres were given, so i am asking for question 5(or the answer for the question that was NOT solved because it was not referenced.) These were the following answers given to me from the last person on bartleby who answered my question without referencing whether it was the answer for question 4 or 5. 1 pass 2 fail 3 fail 4 passarrow_forwardI need question 10 answered please and thank you. Question pertains to the print provided and also the sequence of operations listed in the directions.arrow_forward
- LESSON: AUTODESK AUTOCAD Choose from the choices:arrow_forwardPlease walk me to find the answer and please include the magnitude of the force.arrow_forwardQuestion 23 Given an initial velocity of o ft/s, what is the velocity at 5 seconds? -2 Time (s) -1 ft/s 1 ft/s -11 ft/s 11 ft/s Not enough information Acceleration (ft/s²)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY

Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY