
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
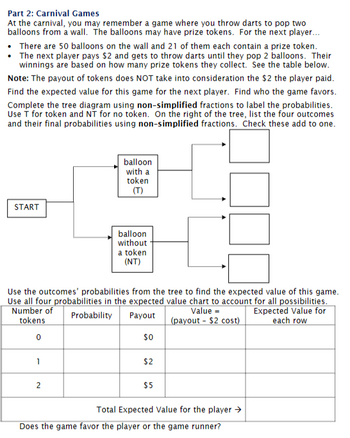
Transcribed Image Text:Part 2: Carnival Games
At the carnival, you may remember a game where you throw darts to pop two
balloons from a wall. The balloons may have prize tokens. For the next player...
• There are 50 balloons on the wall and 21 of them each contain a prize token.
• The next player pays $2 and gets to throw darts until they pop 2 balloons. Their
winnings are based on how many prize tokens they collect. See the table below.
Note: The payout of tokens does NOT take into consideration the $2 the player paid.
Find the expected value for this game for the next player. Find who the game favors.
Complete the tree diagram using non-simplified fractions to label the probabilities.
Use T for token and NT for no token. On the right of the tree, list the four outcomes
and their final probabilities using non-simplified fractions. Check these add to one.
START
1
balloon
with a
token
(T)
Use the outcomes' probabilities from the tree to find the expected value of this game.
Use all four probabilities in the expected value chart to account for all possibilities.
Number of
Expected Value for
tokens
each row
Probability Payout
Value =
(payout - $2 cost)
0
$0
2
balloon
without
a token
(NT)
$2
$5
Total Expected Value for the player →
Does the game favor the player or the game runner?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 2 images

Knowledge Booster
Similar questions
- A teacher wants to assign 4 different tasks to her 4 students. In how many possible ways can she do it? a.24 b. 12 c. 6 d. 42arrow_forwardA game involves drawing a single card from a standard deck. The player receives $10 for an ace, $5 for a king, and $1 for a red card that is neither an ace nor a king. Otherwise, the player receives nothing. If the cost of each draw is $2, should you play? Explain your answer mathematically.arrow_forwardPlease show all work for this problemarrow_forward
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
