P R P'
To understand rigid-body rotation about a translating axis.
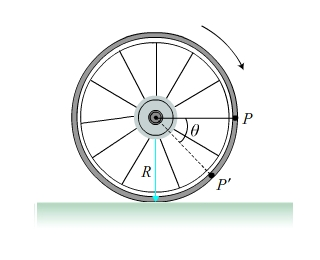
An exhausted bicyclist pedals somewhat erratically. The angular velocity of the front tire, as measured with respect to an axis fixed at the tire’s center, is given by
ω(t)=12t−14sin(2t) for t≥0
where t represents the time in seconds and ω(t) is measured in radians per second. Assume that the tires roll without slipping
The bicycle’s front tire has a spot of paint on it. Take the spot’s position at time t=0.00s to be at angle θ=0.00 radians with respect to an axis parallel to the ground (and perpendicular to the axis fixed at the tire’s center) and take angles in the direction of the tire's rotation to be positive. What angular displacement θ(2) has the spot undergone between 0.00 and 2.0 s? If the tire’s radius is 23 cm, what is d, the magnitude of the spot’s displacement after 2.0 seconds? Which one of the following statements describes the spot’s motion at t=2.0s? The wheel’s angular acceleration is
|
constant and the angular velocity’s magnitude is decreasing. |
|
constant and the angular velocity’s magnitude is increasing. |
|
positive and the angular velocity’s magnitude is decreasing. |
|
positive and the angular velocity’s magnitude is increasing. |
|
negative and the angular velocity’s magnitude is decreasing. |
|
negative and the angular velocity’s magnitude is increasing. |
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images
