College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Question
How can find g? And what does it mean to compare my results to the actual value of 9.80 m/sec2
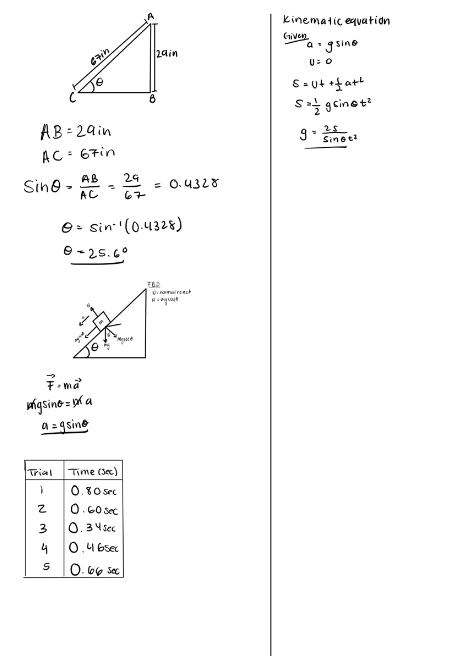
![### Transcript for Educational Website
#### Diagram and Calculations
**Triangle Diagram:**
- A right triangle with:
- Side \( AB = 29 \, \text{in} \)
- Side \( AC = 67 \, \text{in} \)
**Trigonometric Calculations:**
- \[
\sin \theta = \frac{AB}{AC} = \frac{29}{67} = 0.4328
\]
- \[
\theta = \sin^{-1}(0.4328) = 25.6^\circ
\]
#### Inclined Plane Diagram
- **FBD** (Free Body Diagram):
- \( N \): normal reaction
- \( W \): weight
- \( mg \sin \theta \): component of weight down the plane
**Newton's Second Law:**
- \[
F = ma
\]
- \[
mg \sin \theta = mka
\]
- \[
a = g \sin \theta
\]
#### Table of Trials
| Trial | Time (Sec) |
|-------|------------|
| 1 | 0.80 sec |
| 2 | 0.60 sec |
| 3 | 0.34 sec |
| 4 | 0.16 sec |
| 5 | 0.66 sec |
#### Kinematic Equations
- **Given:**
- \( a = g \sin \theta \)
- \( u = 0 \)
- **Equations:**
- \( S = ut + \frac{1}{2} at^2 \)
- \( S = \frac{1}{2} g \sin \theta t^2 \)
- \( g = \frac{2S}{\sin \theta t^2} \)
This information provides a detailed analysis of an object on an inclined plane, demonstrating calculations involving trigonometry, Newton's Laws, and kinematic equations. The experimental trials and times can be used for further analysis or validation of theoretical principles.](https://content.bartleby.com/qna-images/question/560885b1-95a6-46a1-8479-9132da42c8bd/dd2a6bc3-6bf1-4b5b-b9ac-6d97e7f8a2a6/e0qv0ha_processed.jpeg)
Transcribed Image Text:### Transcript for Educational Website
#### Diagram and Calculations
**Triangle Diagram:**
- A right triangle with:
- Side \( AB = 29 \, \text{in} \)
- Side \( AC = 67 \, \text{in} \)
**Trigonometric Calculations:**
- \[
\sin \theta = \frac{AB}{AC} = \frac{29}{67} = 0.4328
\]
- \[
\theta = \sin^{-1}(0.4328) = 25.6^\circ
\]
#### Inclined Plane Diagram
- **FBD** (Free Body Diagram):
- \( N \): normal reaction
- \( W \): weight
- \( mg \sin \theta \): component of weight down the plane
**Newton's Second Law:**
- \[
F = ma
\]
- \[
mg \sin \theta = mka
\]
- \[
a = g \sin \theta
\]
#### Table of Trials
| Trial | Time (Sec) |
|-------|------------|
| 1 | 0.80 sec |
| 2 | 0.60 sec |
| 3 | 0.34 sec |
| 4 | 0.16 sec |
| 5 | 0.66 sec |
#### Kinematic Equations
- **Given:**
- \( a = g \sin \theta \)
- \( u = 0 \)
- **Equations:**
- \( S = ut + \frac{1}{2} at^2 \)
- \( S = \frac{1}{2} g \sin \theta t^2 \)
- \( g = \frac{2S}{\sin \theta t^2} \)
This information provides a detailed analysis of an object on an inclined plane, demonstrating calculations involving trigonometry, Newton's Laws, and kinematic equations. The experimental trials and times can be used for further analysis or validation of theoretical principles.
![**Experiment 2:**
Find a smooth surface that is positioned at an angle (a long board, a slide at a playground, a sloped driveway, etc.). Measure the distance from the starting point up the hill to the finishing point down the hill. Place a smooth running toy at the top of the hill, and let go. Measure the time it takes for the toy to roll down to the bottom of the hill. Repeat 4 more times. Use the middle of the 5 measurements for your calculations. Use the equation:
\[ a = g \sin(\theta) \]
to find the acceleration due to gravity. Of course you’ll need the equations of kinematics to determine the acceleration “a” first before finding \( g \). Again compare your result to the actual value of 9.80 m/sec\(^2\).](https://content.bartleby.com/qna-images/question/560885b1-95a6-46a1-8479-9132da42c8bd/dd2a6bc3-6bf1-4b5b-b9ac-6d97e7f8a2a6/gqloxzo_processed.jpeg)
Transcribed Image Text:**Experiment 2:**
Find a smooth surface that is positioned at an angle (a long board, a slide at a playground, a sloped driveway, etc.). Measure the distance from the starting point up the hill to the finishing point down the hill. Place a smooth running toy at the top of the hill, and let go. Measure the time it takes for the toy to roll down to the bottom of the hill. Repeat 4 more times. Use the middle of the 5 measurements for your calculations. Use the equation:
\[ a = g \sin(\theta) \]
to find the acceleration due to gravity. Of course you’ll need the equations of kinematics to determine the acceleration “a” first before finding \( g \). Again compare your result to the actual value of 9.80 m/sec\(^2\).
Expert Solution
arrow_forward
Step 1
Going through your solution, i see you have done it correctly throughout you need to convert inches in meters and taking time t=0.34 s as per your you'll get the answer.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Similar questions
- I need help on this question. Could you please draw a diagram. Could you also explain how your answers are reasonable and explain whether the answers are reasonable relative to the context provided in the question?arrow_forwardPlease answer the following question(s): 1. Calculate the angle a person needs to lean from the vertical when 1. walking a 17 m (radius) circular track at 22 mins per mile, and Enter to 2 significant figures Angle with respect to the vertical = = 2. running at 4 min per mile. Enter to 2 significant figures Angle with respect to the vertical = Use 1 mile = 1609.4 m ✓ O Oarrow_forwardPlease help. This problem involves finding the radius and volume of a platinum atom using its density. Thank you.arrow_forward
- Provide your calculations, including all relevant steps are included and your units are labeled. The plane carrying the supplies will be cruising at a constant velocity of 250 miles per hour relative to the ground and at a height of 2,650 meters above the target site. Using this information, create a supply drop plan including all required information and calculations outlined below. As you are completing your supply drop plan, remember that correct SI units are a required component of your calculations and descriptions. A) Provide your calculations, including all relevant steps are included and your units are labeled. B) Describe the components of the kinematics equations used in your initial calculations below.arrow_forwardNeeds Complete typed solution with 100 % accuracy.arrow_forward1. The floor of a rectangular building has an area of 120 square meter. The length of the floor / is 4m bigger than its width, w. Solve for I. Hint: Start with the equation of the area in terms of I. What kind of equation do you get? /= 48.11 X feet ! No, that's not the correct answer.arrow_forward
- You will deal with a spherical shell -- a ball, where all the mass is on the surface. Inside is vacuum. (This is difficult to draw other than a circle.) Calculate the surface density (areal density) in g/cm2. You need these numbers: R = 27 cm M = 21,000 gramsarrow_forwardThe volume of air in one beach ball is 972? in3. What is the volume of air in a ball whose radius is 3 inches greater than the first beach ball? A beach ball is spherical in shape. Recall that the formula for the volume V of a sphere where r is the radius is given by the following formula. V=4/3?r3 It is given that the volume of the first beach ball is 972? in3. Substitute this value for V in the volume formula for a sphere. ______= 4/3?r3arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON