
Concept explainers
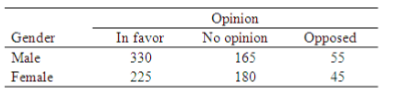
A student organization is trying to decide whether or not to offer more movies on campus. They want to determine whether this idea will appeal to members of both genders. A random sample of 1000 students was asked if they were in favor of more movies on campus. The results by gender are shown in the table below in Figure 2.
Fig. 2: Summary
(a) What proportion of the sampled students is in favor of more movies on campus? (b) What proportion of the sampled females is in favor of more movies on campus? (c) What proportion of the sampled males is in favor of more movies on campus? (d) To answer the original question regarding whether or not to offer more movies on campus, which distribution should the student organization study? i. The joint distribution of gender and opinion.
ii. The marginal distribution of gender. iii. The conditional distribution of gender given opinion. iv. The conditional distribution of opinion given gender.
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

- Each customer entering a department store will either buy or not buy some merchandise. An experiment consists of following 5 customers and determining whether or not they purchase any merchandise. What is the number of sample points in the experiment?arrow_forwardA sample of 296 students at a university is surveyed. The students are classified according to gender ("female" or "male"). They are also classified according to major ("biology", "business", "engineering", "mathematics", or "computer science"). The results are given in the contingency table below. Biology Business Engineering Mathematics Female 33 30 22 45 Male 24 43 26 16 Among all the students in the sample, what is the relative frequency of male computer science majors? Round your answer to two decimal places. 1 X Computer science 41 16 Españ Aaarrow_forwardAmerican businesses provide?" The distribution of responses to this question was as follows: Excellent 8% Pretty good 47% Only fair 34% Poor 11% Suppose a store manager wants to find out whether the results of this consumer survey apply to customers of supermarkets in his city. To do so, he interviews 207 randomly selected customers as they leave the supermarkets in various parts of the city as to their rating of service. Following is the number of responses and distribution of this survey: Excellent 21 Pretty good 109 Only fair 62 Poor 15 Please answer the following: Determine whether the observed frequencies of responses from this survey are statistically the same as the frequencies that would be expected on the basis of the national survey. Hint: Think goodness-of-fit. Also, check out my attachment. Can you describe a chi-squared application, either goodness-of-fit or test-for-independence, in your…arrow_forward
- 6) Do a hypothesis for the following, make sure to include and label all five steps: In a random sample of 600 disks have 35 that are found to be defective. At 0.01 level of significance test the claim that only 1% are defective.arrow_forward3. A newly graduate of administration of justice has been hired by the regional director of the FBI to take a poll of a residential area to determine the proportion of residents who would be opposed to a gun exchange program in their community. The regional director of the FBI told her that if 50% or more of the residents are opposed to the idea, a gun exchange program will not be implemented. She takes a random sample of 150 household heads in the community and find that .42 of those sampled are opposed to the idea. Build a 99% confidence interval around this point estimate. Is 50% within her interval? What would she advise the regional director of the FBI who hired her?arrow_forwardIn a Gallup poll of 1236 adult respondents, 6% said that bad luck follows breaking a mirror. That percentage has a margin of error of 1.5 percentage points. Why is it misleading to state that the percentage is 6% with a margin of error of 1.5%?arrow_forward
- 2. A study for adverse reactions assigned adults at random to one of two common pain relievers (ibuprofen and acetaminophen). It was found that out of 733 adults who were administered ibuprofen, 103 of them experienced an adverse reaction, and out of 732 adults who were administered acetaminophen, 85 of them experienced an adverse reaction. Let p1 denote the proportion of adults who experience an adverse reaction when taking ibuprofen and let p2 denote the proportion of adults who experience an adverse reaction when taking acetaminophen. Suppose we want to answer the following questions. i) Test, at the 3% level of significance, whether the proportion of adults who experience an adverse reaction when taking ibuprofen is greater than the proportion of adults who experience an adverse reaction when taking acetaminophen. ii) Calculate the 97% confidence interval for p1 - P2. The table below provides the information needed to perform the hypothesis test: Value x1 103.0000 85.0000 733.0000…arrow_forwardFrom the given scenario, define the population proportion. In 2019, a national survey organization asked the question "Do you go on more than two vacations per year?" to a random sample of 2,000 Americans. 580 responded "Yes", while the other 1,420 people responded "No". Group of answer choices: A) the proportions of the sampled Americans who go on more than two vacations per year B) the proportion of all Americans who go on more than two vacations per year C) the 1,420 people who responded "No" D) the 2,000 Americansarrow_forwardA sample of 349 students at a university is surveyed. The students are classified according to gender ("female" or "male"). They are also classified according to major ("biology", "business", "engineering", "mathematics", or "computer science"). The results are given in the contingency table below. Biology Business Engineering Mathematics Computer science Female 40 24 33 44 32 Male 29 35 32 37 43 What is the relative frequency of female students in the sample? Round your answer to two decimal places. 0 X S ?arrow_forward
- In 1942, an organization surveyed 1100 adults and asked, "Are you a total abstainer from, or do you on occasion consume, alcoholic beverages?" Of the 1100 adults surveyed, 440 indicated that they were total abstainers. In a recent survey, the same question was asked of 1100 adults and 418 indicated that they were total abstainers. Complete parts (a) and (b) below. (a) Determine the sample proportion for each sample. and respectively. The proportions of the adults who took the 1942 survey and the recent survey who were total abstainers are (Round to three decimal places as needed.)arrow_forward2. A study for adverse reactions assigned adults at random to one of two common pain relievers (ibuprofen and acetaminophen). It was found that out of 733 adults who were administered ibuprofen, 103 of them experienced an adverse reaction, and out of 732 adults who were administered acetaminophen, 85 of them experienced an adverse reaction. Let p1 denote the proportion of adults who experience an adverse reaction when taking ibuprofen and let p2 denote the proportion of adults who experience an adverse reaction when taking acetaminophen. Suppose we want to answer the following questions. i) Test, at the 3% level of significance, whether the proportion of adults who experience an adverse reaction when taking ibuprofen is greater than the proportion of adults who experience an adverse reaction when taking acetaminophen. ii) Calculate the 97% confidence interval for p1 - P2. The table below provides the information needed to perform the hypothesis test: Value x1 103.0000 85.0000 733.0000…arrow_forward2. A study for adverse reactions assigned adults at random to one of two common pain relievers (ibuprofen and acetaminophen). It was found that out of 733 adults who were administered ibuprofen, 103 of them experienced an adverse reaction, and out of 732 adults who were administered acetaminophen, 85 of them experienced an adverse reaction. Let p1 denote the proportion of adults who experience an adverse reaction when taking ibuprofen and let p2 denote the proportion of adults who experience an adverse reaction when taking acetaminophen. Suppose we want to answer the following questions. i) Test, at the 3% level of significance, whether the proportion of adults who experience an adverse reaction when taking ibuprofen is greater than the proportion of adults who experience an adverse reaction when taking acetaminophen. ii) Calculate the 97% confidence interval for p1 - P2. The table below provides the information needed to perform the hypothesis test: Value x1 103.0000 85.0000 733.0000…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





