
Concept explainers
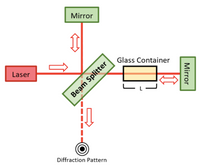
One way to determine the index of refraction of a gas is to use an interferometer. As shown below, one of the beams of an interferometer passes through a glass container that has a length of L = 1.8 cm. Initially the glass container is a vacuum. When gas is slowly allowed into the container, a total of 6894 dark fringes move past the reference line. The laser has a wavelength of 635 nm (this is the
A.) Determine how many wavelengths will fit into the glass container when it is a vacuum. Since the light passes through the container twice, you need to determine how many wavelengths will fit into a glass container that has a length of 2L.
number of wavelengths (vacuum) =
B.) The number of dark fringes is the difference between the number of wavelengths that fit in the container (length of 2L) when it has gas and the number of wavelengths that fit in the container (length of 2L) when it is a vacuum. Use this knowledge to determine how many wavelengths fit into the container (length of 2L) when it is finished being filled with gas.
number of wavelengths (gas) =
C.) Determine the index of refraction of the gas at its final density. How can you combine your answers for (A) & (B) to take advantage of the formula derived in the Content section?
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

- We have an interferometer set up so that no light is reaching the photodetector (that means there is complete destructive interference at the output of the interferometer). If the wavelength of the laser for the interferometer has a wavelength of 1.0 μm, how far does an arm mirror need to move to get maximum light at the output of the interferometer?arrow_forwardAn optician is performing Young's double-slit experiment for her clients. She directs a beam of laser light to a pair of parallel slits, which are separated by 0.120 mm from each other. The portion of this light that passes through the slits goes on to form an interference pattern upon a screen, which is 4.50 meters distant. The light is characterized by a wavelength of 575 nm. (a) What is the optical path-length difference (in um) that corresponds to the third-order bright fringe on the screen? (This is the third fringe, not counting the central bright band, that one encounters moving from the center out to one side.) 1.73*10**3 um Enter a number. (b) What path-length difference (in um) corresponds to the third dark fringe that one encounters when moving out to one side of the central bright fringe? umarrow_forwardThe Rayleigh criterion provides a convenient way to describe the theoretical resolution (e.g. an ability to distinguish two bright objects ) of an optical system. The criterion states that two small bright sources of light can be resolved if the first diffraction minimum of the image of one source point just coincides with of further apart then the first maximum of another (see figure below). A converging lens, 22.8 mm in diameter, is used to form images of distant objects. Considering the diffraction by the lens, what angular separation must two distant point objects have in order to satisfy Rayleigh's criterion? Assume that the wavelength of the light from the distant objects is 640 nm. Provide your Page 1 answer in millidegrees (mdeg).arrow_forward
- The Rayleigh criterion provides a convenient way to describe the theoretical resolution (e.g. an ability to distinguish two bright objects ) of an optical system. The criterion states that two small bright sources of light can be resolved if the first diffraction minimum of the image of one source point just coincides with of further apart then the first maximum of another (see figure below). A converging lens, 31.5 mm in diameter, is used to form images of distant objects. Considering the diffraction by the lens, what angular separation must two distant point objects have in order to satisfy Rayleigh's criterion? Assume that the wavelength of the light from the distant objects is 516 nm. Provide your answer in millidegrees (mdeg).arrow_forwardA plano-convex lens with radius of curvature R = 3.2 m is in contact with a flat plate of glass. A light source and the observer's eye are both close to the normal, as shown in the figure below. The radius of the 51st bright Newton's ring is found to be 9.4 mm. What is the wavelength of the light produced by the source? nm 2//1 Need Help? Read It 8:36 PM 4/11/2021arrow_forwardThe Rayleigh criterion provides a convenient way to describe the theoretical resolution (e.g. an ability to distinguish two bright objects ) of an optical system. The criterion states that two small bright sources of light can be resolved if the first diffraction minimum of the image of one source point just coincides with of further apart then the first maximum of another (see figure below). A converging lens, 34.2 mm in diameter, is used to form images of distant objects. Considering the diffraction by the lens, what angular separation must two distant point objects have in order to satisfy Rayleigh's criterion? Assume that the wavelength of the light from the distant objects is 431 nm. Provide your answer in millidegrees (mdeg). Answer: Choose... +arrow_forward
- A coating is being applied to reduce the reflectivity of a pane of glass to light with a frequency of 4.14 × 10¹4 Hz that is incident normally on the pane. If the material has an index of refraction of 1.34 and the glass has an index of refraction of 1.537, what is the minimum thickness the coating should have in nanometers? Please keep one decimal place in your answer. (c = 3.00 × 108 m/s)arrow_forwardA beam of light of wavelength 691 nm passes through two closely spaced glass plates, as shown in the figure.For what minimum nonzero value of the plate separation d will the transmitted light be bright? (This arrangement is often used to measure the wavelength of light and is called a Fabry-Perot interferometer.)arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





