
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
On Wikipedia it said the proportion of people who bite their nails is over 31%. You aren't sure if you can believe Wikipedia, so you randomly sample 209 people and find 83 of them bite their nails. The hypothesis test with α=0.05 had a p-value of 0.0033, which causes you to reject the null, and believe that Wikipedia was right. Assuming the true proportion really was 0.31, if another sample of 209 people was taken, what is the probability of getting a proportion as high as 83/209 or higher?
Expert Solution
arrow_forward
Step 1
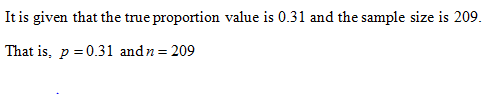
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- USA Today reported that about 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice. Suppose Chevrolet did a study of a random sample of 1007 Chevrolet owners and found that 484 said they would buy another Chevrolet. Does this indicate that the population proportion of consumers loyal to Chevrolet is more than 47%? Use α = 0.01. 1. What is the value of the sample test statistic? (Round your answer to two decimal places.) 2. Find the P-value of the test statistic. (Round your answer to four decimal places.)arrow_forward12% of all Americans suffer from sleep apnea. A researcher suspects that a lower percentage of those who live in the inner city have sleep apnea. Of the 335 people from the inner city surveyed, 34 of them suffered from sleep apnea. What can be concluded at the level of significance of a = 0.01? a. For this study, we should use z-test for a population proportion ♥ b. The null and alternative hypotheses would be: Ho: ? Select an answer |(please enter a decimal) Hạ ?v Select an answer ♥ (Please enter a decimal) c. The test statistic ?v = (please show your answer to 4 decimal places.) d. The p-value = (Please show your answer to 4 decimal places.) e. The p-value is f. Based on this, we should fail to reject the null hypothesis. g. Thus, the final conclusion is that. O The data suggest the populaton proportion is significantly smaller than 12% at a= 0.01, so there is sufficient evidence to conclude that the population proportion of inner city residents who have sleep apnea is smaller than…arrow_forwardI have read that 20% of undergraduate students experience food insecurity sometime during each academic year. I wish to test if this is true at a particular university. I plan the following experiment. I will randomly sample 100 students at the university and compute the proportion of them who have experienced food insecurity during the last year; this proportion is p-hat. If p-hat ≤ 0.12 or p-hat ≥ 0.28, I will decide that the proportion of students experiencing food insecurity during the last year was not equal to 0.20. Otherwise, I will decide I cannot conclude it was different from 0.20. When I run the trial, I find 15 of the 100 students experienced food insecurity during the previous year, so p-hat = 0.15. Take the following probabilities as given; you do not need to check them. They provide all the information you need in order to answer the first section of questions. Let p be the proportion of students who experience food insecurity each year at the university. If p=0.20,…arrow_forward
- The 2006 Statistical Abstract of the United States reports on a survey that asked a national sample of 80,000 American households about pet ownership. Suppose (for now) that one-third of all American households own a pet cat. This survey found that 32.8% of the households sampled owned a pet cat. Is this number a parameter or a statistic? Calculate the Z-score of this sample proportion (0.328).arrow_forwardA hypothesis test was performed to decide whether the mean number of words spoken per day by men is fewer than for women. αα = 0.05 and p = 0.02. If a man and a woman are randomly selected there is a 2% chance that the man will speak fewer words than the woman on that day.arrow_forwardA physical therapist wanted to know whether the mean step pulse of men was less than the mean step pulse of women. She randomly selected 52 men and 73 women to participate in the study. Each subject was required to step up and down a 6-inch platform. The pulse of each subject was then recorded. The following results were obtained. (a) State the null and alternative hypotheses. Which of the following is correct? OC. Hgi H1 =H2i H H2 (b) Identify the P-value and state the researcher's conclusion if the level of significance was a = 0.02. What is the P-value? P.value =arrow_forward
- Based on information from a previous study, r1 = 34 people out of a random sample of n1 = 105 adult Americans who did not attend college believe in extraterrestrials. However, out of a random sample of n2 = 105 adult Americans who did attend college, r2 = 50 claim that they believe in extraterrestrials. Does this indicate that the proportion of people who attended college and who believe in extraterrestrials is higher than the proportion who did not attend college? Use ? = 0.01. (a) What is the level of significance?State the null and alternate hypotheses. H0: p1 = p2; H1: p1 ≠ p2H0: p1 < p2; H1: p1 = p2 H0: p1 = p2; H1: p1 < p2H0: p1 = p2; H1: p1 > p2 (b) What sampling distribution will you use? What assumptions are you making? The Student's t. The number of trials is sufficiently large.The standard normal. We assume the population distributions are approximately normal. The standard normal. The number of trials is sufficiently large.The Student's t. We assume the…arrow_forward10% of all Americans suffer from sleep apnea. A researcher suspects that a lower percentage of those who live in the inner city have sleep apnea. Of the 369 people from the inner city surveyed, 22 of them suffered from sleep apnea. What can be concluded at the level of significance of αα = 0.01? For this study, we should use Select an answer t-test for a population mean z-test for a population proportion The null and alternative hypotheses would be: Ho: ? μ p Select an answer = < ≠ > (please enter a decimal) H1: ? μ p Select an answer > ≠ < = (Please enter a decimal) The test statistic ? z t = (please show your answer to 3 decimal places.) The p-value = (Please show your answer to 4 decimal places.) The p-value is ? > ≤ αα Based on this, we should Select an answer reject accept fail to reject the null hypothesis. Thus, the final conclusion is that ... The data suggest the population proportion is not significantly smaller than 10% at αα = 0.01, so…arrow_forwardSome people say that more babies are born in September than in any other month. To test this claim, you take a random sample of 150 students at your school and find that 21 of them were born in September. You are interested in whether the proportion born in September is greater than 1/12-what you would expect if September was no different from any other month. Thus, the null hypothesis is Ho: p=1/12 . The P-value for your test is 0.0056. Which of the following statements correctly interprets the P-value? Assuming that the proportion of babies born in September is greater than any other month, there is a 0.0056 probability of getting a sample proportion of 21/150 or greater by chance alone. Assuming that the proportion of babies born in September is the same as any other month, there is a 0.0056 probability of getting a sample proportion of 21/150 or greater by chance alone. The probability that the proportion of September birthdays is not equal to 1/12 is 0.0056. The probability that…arrow_forward
- The population of healthy female adults, the mean red blood cell count (RBC) is 4.8 (millions of cells per cubic millimeter of whole blood). A researcher thinks the RBC is underestimated, so she conducts a test of significance using Null Hypothesis: µ ≤ 4.8 vs. Alternative Hypothesis: µ >4.8. If the true mean RBC is 4.75 and the null hypothesis is rejected, out of the four options below, what has occured? Type 1 Error, Type 2 Error, No error, OR can’t tell without knowing the degrees of freedom?arrow_forwardA researcher belleves that 52% of people who grew up as the only child have an IQ score over 100. However, unknown to the researcher, this figure is actually 50%, which is the same as in the general population. To attempt to find evidence for the claim, the researcher is going to take a random sample of 400 people who grew up as the only child. Let p be the proportion of people in the sample with an IQ score above 100. Answer the following. (If necessary, consult a list of formulas.) (a) Find the mean of p. (b) Find the standard deviation of p. (c) Compute an approximation for P(p 20.52), which is the probability that there will be 52% or more people with IQ Scores over 100 in the sample. Round your answer to four decimal places. 2022 acerarrow_forward16% of all Americans suffer from sleep apnea. A researcher suspects that a different percentage of those who live in the inner city have sleep apnea. Of the 337 people from the inner city surveyed, 47 of them suffered from sleep apnea. What can be concluded at the level of significance of α= 0.05? a. The test statistic= (please show your answer to 3 decimal places.) b. The p-value = (Please show your answer to 4 decimal places.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
