Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
![**Question:**
On what region of the xy-plane does the differential equation have a unique solution that satisfies the given initial condition?
\[
(9 - y^2)y' = x^2, \quad y(-3) = -4
\]
**Options:**
a. A unique solution exists in the regions \( y < -3 \).
b. A unique solution exists in the region \( y \neq \pm 3 \).
c. A unique solution exists in the region consisting of all points in the xy-plane except \((0,3)\) and \((0,-3)\).
d. A unique solution exists in the region \(-3 < y < 3\).
e. A unique solution exists in the entire xy-plane.](https://content.bartleby.com/qna-images/question/1300845a-828a-484d-8f06-319293900125/1ba386ec-a12c-47f6-a8f2-d28533479282/6jucte_processed.png)
Transcribed Image Text:**Question:**
On what region of the xy-plane does the differential equation have a unique solution that satisfies the given initial condition?
\[
(9 - y^2)y' = x^2, \quad y(-3) = -4
\]
**Options:**
a. A unique solution exists in the regions \( y < -3 \).
b. A unique solution exists in the region \( y \neq \pm 3 \).
c. A unique solution exists in the region consisting of all points in the xy-plane except \((0,3)\) and \((0,-3)\).
d. A unique solution exists in the region \(-3 < y < 3\).
e. A unique solution exists in the entire xy-plane.
Expert Solution
arrow_forward
Step 1
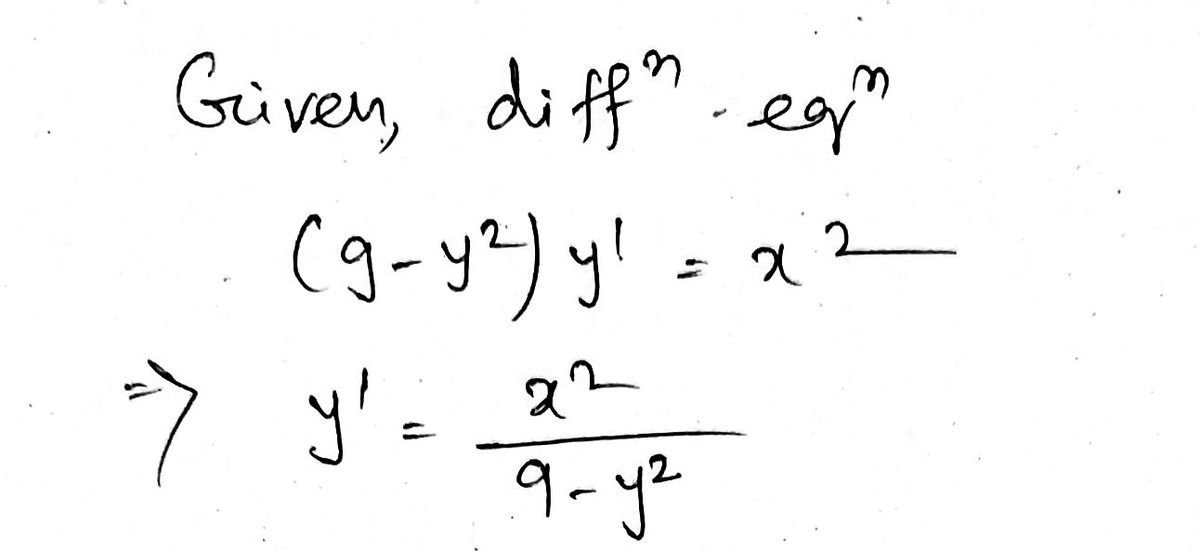
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- The given family of functions is the solution general of the differential equation on the indicated interval. Find a family member who is a solution to the initial value problem.arrow_forwarddy = y' (1-y*) Given the autonomous first-order differential equation c) By hand, sketch typical solution curves in the region in the xy-plane determined by the graphs of the equilibrium solutions. 2.arrow_forwardFind a homogeneous linear differential equation with constant coefficients whose general solution is given. 3x y = C₁ + ₂x + c₂e³x Oy"" - 3y" = 0 y"" + 3y" = 0 y" - 4y" + 3y' = 0 y"" + 3y¹ = 0 Oy" + 4y" + 3y' = 0arrow_forward
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,