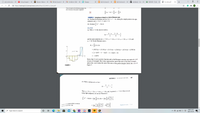
O edcc.instructure X O Acing Google Co x O Kevawn Redund x M Whole Course Re x M Invitation: CS& x e Papago C Get Homework X C Get Homework X O variables2 - Solv x WAMAP - Posts X O 52 Calc.paf i https://wamaps3.s3.amazonaws.com/ufiles/222249/5.2 Calc.pdf These are equal by the datrbutve property The other formulas are discussed in Acpends 11 È la, - b.) = E a, – É b, EXAMPLE 2 Evaluating an integral as a limit of Riemann sums (a) Evaluate the Riemann sum for f(x) -x' - 6x, taking the sample points to be right endpoints and a - 0, b-3, and a -6. (b) Evaluate '(r' - 6x) dx. SOLUTION (a) With a-6 the interval width is -a3-0 Ar= Ar- 6 and the right endpoints are x, - 0.5. x: = 1.0, x = 1.5, x. - 2.0. xs = 25, and X - 3.0. So the Riemann sum is R, - E fLr,) Ar - S(0.5) Ar + S(1.0) ar + f(1.5) Ar + f(2.0) Ar + f(2.5) Ar + f(3.0) Ax y'-f -(-2.875 - 5 - 5.625 - 4 + 0.625 + 9) - -3.9375 Notice that f is not a positive function and so the Riemann sum does not represent a sum of areas of rectangles. But it does represent the sum of the areas of the blue rectangles (above the x-axis) minus the sum of the areas of the gold rectangles (below the x-aisi in Figure 5. FIGURE S 347 SECTION S2 HE DEFINITE INIEGRAL th) With a suhintervals we have Thus X0, x - yn, x;- 6/n, , 9/n, and, in general, x,- 3i/n. Since we are using right endpoints, we can use Theorem 4: C - 6z) dr = lim E fix.) Ar - lim a Constant unike il so we can ientont of the sign - lim - P Type here to search O Ei A O A 40 ® 한 2 12:57 局 2021-01-07

Basketball Scoreb X + udentFunctions/Interface/acellus_engine.html?ClassID=1238572784# /selectclass.html Find the area of this triangle. 11 16 Copyright © 2003-2023 International Academy of Science. All Rights Reserved. [?] square units Round to the nearest tenth. GET UN DAFFDE BE 13 F10 LG F11 J 25% F12 prt sc bys ro Enter pause break C page

G Gmail Bb Pearson's MyLab & Mastering x Do Homework - L05 Homewor x AG 2021-2022 Aggie Gentz Book x Award History + A mathxl.com/Student/PlayerHomework.aspx?homeworkld=591061310&questionld=17&flushed=false&cld=6387569&back=https://www.mathxl.com/. I Apps Is Mesh Contrast Sh.. s Frill Neck Semi Sh.. S Sheer Mesh Long.. C Kinky Curly Wefte. R dress O money in marriage A Other Bookmarks Math132-003 (Calculus II - 2021S) Online - Clemence Makala Langley & | 02/18/21 2:50 PM Homework: L05 Homework: Trig Substitution Save Score: 0 of 1 pt 25 of 27 (23 complete) v HW Score: 79.63%, 21.5 of 27 pts 8.4.68-Setup & Solve Question Help ▼ Evaluate the following integral. dx V(x - 1)(7 - x) Rewrite the radicand by completing the square and simplifying. -S dx dx V(x- 1)(7- x) Enter your answer in the answer box and then click Check Answer. parts remainina Check Answer Clear All javascript:doExercise(25);

Image attached with question