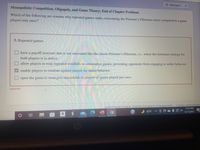
O Attempt 1 Monopolistic Competition, Oligopoly, and Game Theory: End of Chapter Problems Which of the following are reasons why repeated games make overcoming the Prisoner's Dilemma easier compared to a game played only once? 5. Repeated games have a payoff structure that is not structured like the classic Prisoner's Dilemma, i.e., where the dominant strategy for both players is to defect. O allow players to reap repeated windfalls in consecutive games, preventing opponents from engaging in unfair behavior. enable players to retaliate against players for unfair behavior. open the game to strategies unavailable to players of games played just once. Incorrect

7.

in this game table, Pepsi's payout is on the left and Sam's Choice's is on the ight. Is the Nash equilibrium a prisoner's dilemma? Pepsi High Low Sam's Choice High 110, 20 60, 10 Low 80, 40 70, 30 O No, it is not because both firms played their dominant strategies. O Yes, it is because the combined payoff for the two firms is lower than another outcome. O Yes, it is because at least one of the firms ends up with the lowest possible payoff. O No, it is not because at least one firm has achieved its highest possible payoff.

PART C D

1. Consider the following game matrix. Player A Answer: Top Bottom Left a, b e, f Player B Right c, d g, h (a) If top and left are strictly dominant strategies, then what do we know the relationship of the parameters? (b) If (top, left) is a Nash equilibrium, then what do we know the relationship of the parameters? Answer: (c) If top and left are strictly dominant strategies, will (top, left) be a Nash equilibrium? Why? Answer: (d) If (top, left) is a Nash equilibrium, must the strategies be strictly dominant strategies? Why? Answer:

1. The table below shows a prisoner's dilemma in normal form. Players 1 and 2 each choose between D and C. D C D 2,2 1,10 10, 1 5,5 Answer the following questions. Remember to explain your reasoning. (a) If the game is played only once, what is the equilibrium in dominant strategies? (b) If the game is played three times in a row, what action does each player choose in every round? Suppose that the game is repeated indefinitely. The players do not discount the future. How- ever, the game ends with probability p € (0, 1) after each round. Assume that each player uses the following grim-trigger strategy. Each player chooses C in the first round. Each player chooses C in the current round if both players chose C in every previous round. Each player chooses D in the current round if either player chose D in some previous round. (c) If p = 1, is it optimal for each player to use the grim-trigger strategy above given that the other player uses the grim-trigger strategy above? [Hint: compare…

Question 5 Consider following extensive form game Keep Prices (8,2) Advertise Lower Prices (4,6) O Advertise; Lower Prices Firm 1 O Advertise; Keep Prices Firm 2 O Not Advertise; Keep Prices Not Advertise The subgame perfect Nash-equilibrium is O Not Advertise; Lower Prices Keep Prices (6,10) O Lower Prices (3,7) 5 pts

A 201.

In a game theory payoff matrix. Your company (A) and a major competitor (B) havetwo potential strategies: to advertise or to not advertise during the Super Bowl. The payoffs in each cell represent the change in firm profits from advertising.   How would you create payoffs in each cell such that the Nash equilibrium is that both firms advertise despite having a higher profit if neither firm advertised

12. What is the subgame-perfect outcome from a finitely repeated game? a. Iterated Elimination Outcome played in each stage b. Backwards Induction Outcome played in each stage Nash Equilibrium played in each stage d. Nash Equilibrium in stage 1 only