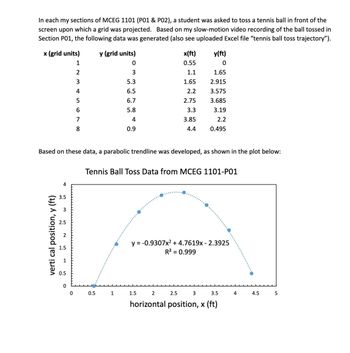
In each my sections of MCEG 1101 (P01 & P02), a student was asked to toss a tennis ball in front of the screen upon which a grid was projected. Based on my slow-motion video recording of the ball tossed in Section P01, the following data was generated (also see uploaded Excel file "tennis ball toss trajectory").| x (grid units) | y (grid units) | x(ft) | y(ft) ||----------------|----------------|-------|-------|| 1 | 0 | 0.55 | 0 || 2 | 3 | 1.1 | 1.65 || 3 | 5.3 | 1.65 | 2.915 || 4 | 6.5 | 2.2 | 3.575 || 5 | 6.7 | 2.75 | 3.685 || 6 | 5.8 | 3.3 | 3.19 || 7 | 4 | 3.85 | 2.2 || 8 | 0.9 | 4.4 | 0.495 |Based on these data, a parabolic trendline was developed, as shown in the plot below:**Tennis Ball Toss Data from MCEG 1101-P01:**A graph is depicted with the following details:- **Title:** Tennis Ball Toss Data from MCEG 1101-P01- **Axes Labels:** - Horizontal axis (x-axis): horizontal position, x (ft), ranging from 0 to 5. - Vertical axis (y-axis): vertical position, y (ft), ranging from 0 to 4.- **Data Points:** Plot shows blue circular markers indicating the data points plotted along with a light blue dotted trendline illustrating the parabolic trajectory of the tennis ball.- **Equation of the Parabola:** The equation of the trendline is \( y = -0.9307x^2 + 4.7619x - 2.3925 \).- **Coefficient of Determination:** \( R^2 = 0.999 \), suggesting a very good fit to the data. Now, assuming negligible aerodynamic drag, the equations governing the "flight" of the ball are given as:\[ x = x_o + V_{ox}t \]\[ y = y_o + V_{oy}t - \frac{1}{2}gt^2 \]The first of these equations can be used to isolate \( t \) and express it as a function of \( x \) (as done in class). Then this expression for \( t \) can be substituted into the second equation to obtain an equation for \( y \) as a function of \( x \) (as done in class). Finally, this equation can be simplified and put into the standard form of:\[ y = ax^2 + bx + c \]Perform this process and compare the result to the trendline equation to determine the "launch" speed of the ball \( V_o \).

Answered: Image /qna-images/answer/fcc9e6ea-6438-4490-88ce-20f7b75de86d.jpg

Now assuming negligible aerodynamic drag, the equations governing the "flight" of the ball are given as: x = xo +Voxt 1 29t² y = yo + Voyt - The first of these equations can be used to isolate t and express it as a function of x (as done in class). Then this expression for t can be substituted into the second equation to obtain an equation for y as a function of x (as done in class). Finally, this equation can be simplified and put into the standard form of: y = ax² + bx + c Perform this process and compare the result to the trendline equation to determine the "launch" speed of the ball Vo.

Now assuming negligible aerodynamic drag, the equations governing the "flight" of the ball are given as: x = xo +Voxt 1 29t² y = yo + Voyt - The first of these equations can be used to isolate t and express it as a function of x (as done in class). Then this expression for t can be substituted into the second equation to obtain an equation for y as a function of x (as done in class). Finally, this equation can be simplified and put into the standard form of: y = ax² + bx + c Perform this process and compare the result to the trendline equation to determine the "launch" speed of the ball Vo.

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Similar questions

The scalar product A · B of the two vectors A = 2i + 3j and B =i- 2j is O -4 k O 2i - 6j -4
Problem 4: Vector Addition. Vector A = 200 NZ45° counterclockwise from the z axis, and vector B = 300 N 270° counterclockwise from the y axis. Find the resultant R= A + B by addition of scalar components. Problem 5: Consider the picture below. Find the tension T, tension Ta tension T₂
Determine the magnitude of the vertical reaction (N) at A if P = 355 N and Q = 2100 N. Let x = 2.45 m, y = 2.56 m, and z = 2.06 m. Round off only on the final answer expressed in 3 decimal places. Instead of units, indicate the direction of the horizontal reaction at A: use R if to the right and L if to the left.
Needs Complete typed solution with 100 % accuracy.
Answer must be in standard form scientific notation with SI units that do not have prefixes ( except for kg.) all angles and directions must be calculated to the nearest 0.1 deg. (Tenth of a degree) and entered in standard form scientific notation.
I do not know how to get started with my graph. Does my x axis need to be between 7.84 or 15.68 and my y axis between 0.779 or 1.558. If so how should I start my graph and how much should I go up by with both x and y axis's. Please help! I am confused.
A vector a of magnitude 17 units and another vector b of magnitude 8.5 units differ in directions by 72°. Find (a) the scalar product of the two vectors and (b) the magnitude of the vector product a×b.
A particle of mass m has a time-dependent position vector r(t) = (Rcos(ωt),Rsin(ωt),αt) in Cartesian coordinates, where R, ω and α are positive constants. What are the physical dimensions of R, ω and α? Show that the speed of the particle is constant. Does it mean that the acceleration is zero? Justify.
V:31) Show that the addition or subtraction of two numbers x and y with the same percent error results in a number z with the same percent error. What is the percent error of z if x has half the percent error of y?
A vector is given by: i = (-2.11) + ( -4.28) ĵ+ ( 2.8 ) k. Determine the component of the unit vector û .
m = 3.0729 3. Consider the digits of your student number 20XY-FAITH. The wooden block (mass kg) is released from rest at A by a compressed spring (compressed length 0.6 m, undeformed length 1 m, spring constant k = 150 N/m). The block is allowed to slide through the rough horizontal surface (A to B), then along the smooth circular ramp (B to C, central angle 0 = 41.5 °), until the block is released after point C. Calculate the speed of the block at points B and C. Also, what is the magnitude of the normal force exerted to the block just before the block leaves the ramp? Neglect the geometry of the block. NOTE: Use Work-Energy Method to solve for the speeds, and use FMA Method to compute for the normal force. 0.6 m mmmmm 3.0729 kg A 1 m rough surface Hs = 0.35 Mk = 0.25 path of the block 1.5 m O B smooth surface Ө 1.5 m C
Part (a) Do this for the range r > R. E = _____ Part (b) Do this for the range r < R. E = _____