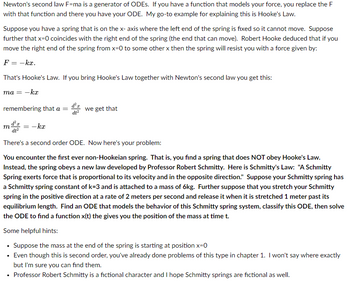
Newton's second law F=ma is a generator of ODES. If you have a function that models your force, you replace the F with that function and there you have your ODE. My go-to example for explaining this is Hooke's Law. Suppose you have a spring that is on the x- axis where the left end of the spring is fixed so it cannot move. Suppose further that x=0 coincides with the right end of the spring (the end that can move). Robert Hooke deduced that if you move the right end of the spring from x=0 to some other x then the spring will resist you with a force given by: F = -kx. That's Hooke's Law. If you bring Hooke's Law together with Newton's second law you get this: ma = -kx remembering that a = m d'r = -kx dt² we get that There's a second order ODE. Now here's your problem: You encounter the first ever non-Hookeian spring. That is, you find a spring that does NOT obey Hooke's Law. Instead, the spring obeys a new law developed by Professor Robert Schmitty. Here is Schmitty's Law: "A Schmitty Spring exerts force that is proportional to its velocity and in the opposite direction." Suppose your Schmitty spring has a Schmitty spring constant of k=3 and is attached to a mass of 6kg. Further suppose that you stretch your Schmitty spring in the positive direction at a rate of 2 meters per second and release it when it is stretched 1 meter past its equilibrium length. Find an ODE that models the behavior of this Schmitty spring system, classify this ODE, then solve the ODE to find a function x(t) the gives you the position of the mass at time t. Some helpful hints: • Suppose the mass at the end of the spring is starting at position x=0 • Even though this is second order, you've already done problems of this type in chapter 1. I won't say where exactly but I'm sure you can find them. • Professor Robert Schmitty is a fictional character and I hope Schmitty springs are fictional as well.

DIFFERENTIAL EQUATIONS  (UPVOTE WILL BE GIVEN. PLEASE WRITE THE COMPLETE SOLUTIONS LEGIBLY AND CHOOSE THE CLOSEST VALUE IN THE CHOICES. NO LONG EXPLANATION NEEDED. . THANK YOU!)