
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Find the root of the function using the following methods.
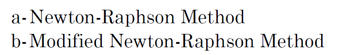
Transcribed Image Text:a-Newton-Raphson Method
b-Modified Newton-Raphson Method
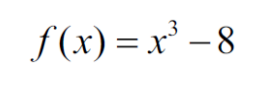
Transcribed Image Text:f(x)=x²³ -8
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- A penny is thrown from the top of a 48.9-meter building and hits the ground 3.04 seconds after it was thrown. The penny reached its maximum height above the ground 0.79 seconds after it was thrown. Define a quadratic function, h, that expresses the height of the penny above the ground (measured in meters) as a function of the number of seconds elapsed since the penny was thrown, t. What is the maximum height of the penny above the ground?arrow_forwardFind the root of the given function using a. Incremental Search Method b. Method of Successive Substitution c. Bisection Method F(x) = x* + 5x – 16x² -2x + 16 Note: 1. Tabulate and compare your results. 2. Use spreadsheets and show graph for the values of x.arrow_forwardFor the following situation: A six foot person standing on a flat surface throws a javelin in the air. After traveling horizontally for 75 feet it reaches a peak height of 81 feet above the surface. a) Create a quadratic function (in any of the three forms) to match this situation. Let z be the horizontal distance in feet and h(r) be the height in feet b) How far horizontally does the javelin travel before it hits the ground? Round to the nearest foot. c) What is the range (all of the output values) of this function in the context of the javelin being thrown?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

