n this exercise we will use the Laplace transform to solve the following initial value problem: y" + 6y' + 9y = 0, y(0) = 1, y' (0) = 1 %3D %3D y(t)
n this exercise we will use the Laplace transform to solve the following initial value problem: y" + 6y' + 9y = 0, y(0) = 1, y' (0) = 1 %3D %3D y(t)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![In this exercise, we will use the Laplace transform to solve the following initial value problem:
\[ y'' + 6y' + 9y = 0, \quad y(0) = 1, \; y'(0) = 1 \]
\[ y(t) = \] *[Input box for the solution]*
This problem involves finding the function \( y(t) \) that satisfies the given differential equation and initial conditions. Using the Laplace transform is a powerful method for handling such problems, especially when dealing with linear differential equations with constant coefficients.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fac965a5e-260b-4b5a-b5dd-dbb137feedb3%2F714a12f1-9db8-424c-a69e-8f70be4c492c%2Fpnluvwk_processed.jpeg&w=3840&q=75)
Transcribed Image Text:In this exercise, we will use the Laplace transform to solve the following initial value problem:
\[ y'' + 6y' + 9y = 0, \quad y(0) = 1, \; y'(0) = 1 \]
\[ y(t) = \] *[Input box for the solution]*
This problem involves finding the function \( y(t) \) that satisfies the given differential equation and initial conditions. Using the Laplace transform is a powerful method for handling such problems, especially when dealing with linear differential equations with constant coefficients.
Expert Solution
Step 1
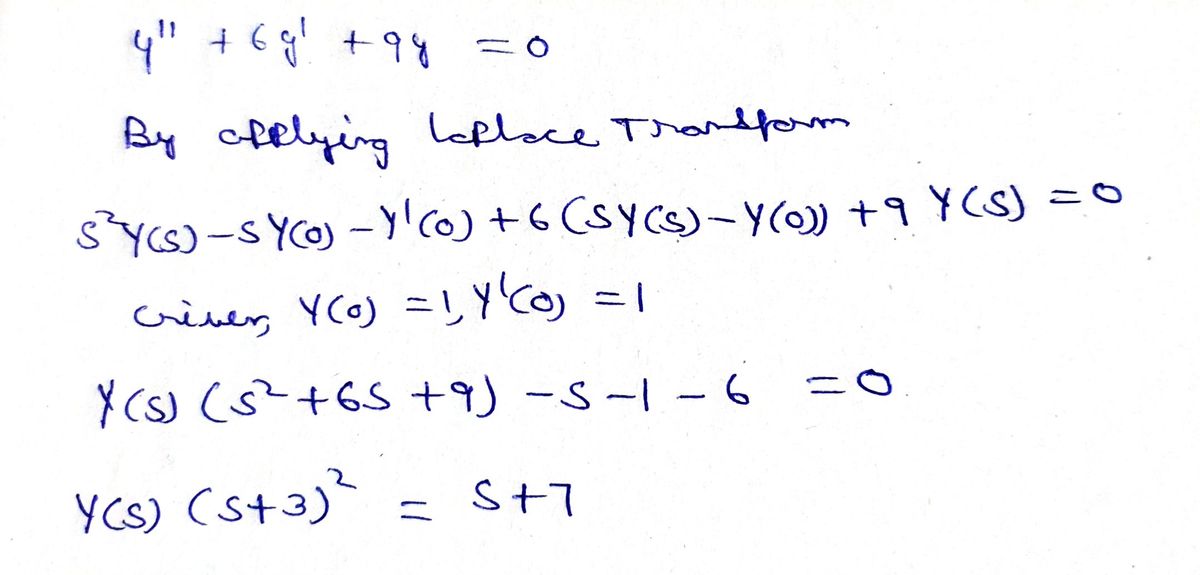
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

