c only please A report classified fatal bicycle accidents according to the month in which the accident occurred, resulting in the accompanying table.P₁P2P3(a) Use the given data to test the null hypothesis Ho: P₁Calculate the test statistic. (Round your answer to two decimal places.)x² = 91.28P4P5P6==What is the P-value for the test? (Use a statistical computer package to calculate the P-value. Round your answer to four decimal places.)P-value = 0=MonthJanuaryFebruaryMarchAprilMayJuneJulyAugustSeptemberOctoberNovemberDecemberWhat can you conclude?Reject Ho. There is not enough evidence to conclude that fatal bicycle accidents are not equally likely to occur in each of the months.Do not reject Ho. There is not enough evidence to conclude that fatal bicycle accidents are not equally likely to occur in each of the months.Reject Ho. There is convincing evidence to conclude that fatal bicycle accidents are not equally likely to occur in each of the months.Do not reject Ho. There is convincing evidence to conclude that fatal bicycle accidents are not equally likely to occur in each of the months.=(b) The null hypothesis in part (a) specifies that fatal accidents were equally likely to occur in any of the 12 months. But not all months have the same number of days. What null and alternative hypotheses would you test to determine if some months are riskier than others if you wanted to take differing month lengthsinto account? (Assume this data was collected during a leap year, with 366 days.)=Identify the null hypothesis by specifying the proportions of accidents we expect to occur in each month if the length of the month is taken into account. (Enter your probabilities as fractions.)31/36629/36631/366P7P8P9P10 =P11P12=Number of Accidents363045597872100=USE SALT87666640385/6131/3665/6131/36631/35/6111231/3665/6131/366112P2, P12112where p₁ is the proportion of fatal bicycle accidents that occur in January, P₂ is the proportion for February, and so on. Use a significance level of 0.01.Identify the correct alternative hypothesis.Ho is not true. None of the proportions is correctly specified under Ho. 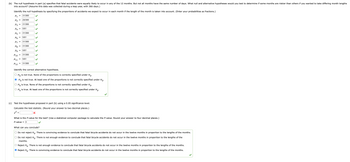(b) The null hypothesis in part (a) specifies that fatal accidents were equally likely to occur in any of the 12 months. But not all months have the same number of days. What null and alternative hypotheses would you test to determine if some months are riskier than others if you wanted to take differing month lengthsinto account? (Assume this data was collected during a leap year, with 366 days.)Identify the null hypothesis by specifying the proportions of accidents we expect to occur in each month if the length of the month is taken into account. (Enter your probabilities as fractions.)P1 31/36629/36631/366P₂P3P4P5P6P7P8=========5/61P9P10 31/366P11 5/61P12 31/366==5/61=31/3665/6131/36631/366Identify the correct alternative hypothesis.O Ho is not true. None of the proportions is correctly specified under Ho.● Ho is not true. At least one of the proportions is not correctly specified under Ho.O Ho is true. None of the proportions is not correctly specified under Ho.O Ho is true. At least one of the proportions is not correctly specified under Ho.(c) Test the hypotheses proposed in part (b) using a 0.05 significance level.Calculate the test statistic. (Round your answer to two decimal places.)x²:What is the P-value for the test? (Use a statistical computer package to calculate the P-value. Round your answer to four decimal places.)P-value = 0What can you conclude?Do not reject Ho. There is convincing evidence to conclude that fatal bicycle accidents do not occur in the twelve months in proportion to the lengths of the months.Do not reject Ho. There is not enough evidence to conclude that fatal bicycle accidents do not occur in the twelve months in proportion to the lengths of themonths.Reject Ho. There is not enough evidence to conclude that fatal bicycle accidents do not occur in the twelve months in proportion to the lengths of the months.O Reject Ho. There is convincing evidence to conclude that fatal bicycle accidents do not occur in the twelve months in proportion to the lengths of the months.

Question

Accepted Answer

By applying the Chi-square test for goodness of fit,
c)
Grand sum (N) = 717
expected  proportion…

Month January February March April May June July August September October November December Number of Accidents 36 30 45 USE SALT 59 78 72 100 87 66 66 40 38 se the given data to test the null hypothesis Mg: P₁ where p, is the proport