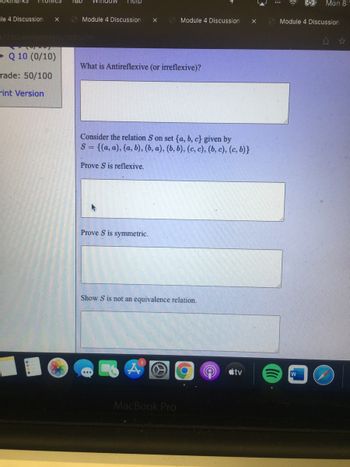
Module 4 Discussion X Module 4 Discussion X What is Antireflexive (or irreflexive)? Consider the relation S on set (a, b, c} given by S = {(a, a),(a, b), (b, a), (b, b), (c, c), (b, c), (c, b)} Prove S is reflexive. Prove S is symmetric. Show S is not an equivalence relation. Module 4 Discuss

Discrete math: please provide me 100% accurate answers

Theorem: Let R ⊆ A × A be a relation. Then R is transitive if and only if R ◦ R ⊆ R. Prove Theorem: show that R is transitive if and only if R ◦ R ⊆ R. No handwritten please

Let R be a relation on A = {0, 3, 4, 7} and R = {(0, 3), (3, 0), (7, 3), (4, 4), (7, 7), (3, 7), (3, 3)}. Are the following statements true or false? ? ? ? ? ? ? 1. R is symmetric ↑ 2. R is anti-symmetric 3. R is transitive ◆ 4. R is reflexive 5. R is a partial order ♦ 6. R is an equivalence relation