
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:Mathematical Problems
sidong cut back
(32.1.) Show that the Madhava-Jyesthadeva formula given at the beginning of the chapter
is equivalent to
or, letting x = tan 0,
0
=(-1) tan24+18
2k + 1
k=0
arctan x=
8
+2k+1
2k + 1
(-1);
k=0
DALE
![The product of the given Sine and the radius divided by the Cosine is the first result. From
the first,... etc., results obtain...a sequence of results by taking repeatedly the square of the
Sine as the multiplier and the square of the Cosine as the divisor. Divide... in order by the odd
numbers one, three, etc... From the sum of the odd terms, subtract the sum of the even terms.
[The result] becomes the arc. [Rajagopal, 1993, p. 98]
These instructions give in words an algorithm that we would write as the following
formula, remembering that the Sine and Cosine used in earlier times correspond to our
r sine and r cos 0, where r is the radius of the circle:
Madhava-
A sin³0
3r3 cos³ 0
re
Jyesthadeva
² sine
formula
r cos 0
The bulk of calculus was developed in Europe during the seventeenth century, and it is
on that development that the rest of this chapter is focused.
6 sine
+
5r5 cos
0](https://content.bartleby.com/qna-images/question/7011b814-0888-4e7c-ad26-86019bf83fb9/b2bfa02c-0122-4133-b10a-47d3259d1e35/233fw7_thumbnail.jpeg)
Transcribed Image Text:The product of the given Sine and the radius divided by the Cosine is the first result. From
the first,... etc., results obtain...a sequence of results by taking repeatedly the square of the
Sine as the multiplier and the square of the Cosine as the divisor. Divide... in order by the odd
numbers one, three, etc... From the sum of the odd terms, subtract the sum of the even terms.
[The result] becomes the arc. [Rajagopal, 1993, p. 98]
These instructions give in words an algorithm that we would write as the following
formula, remembering that the Sine and Cosine used in earlier times correspond to our
r sine and r cos 0, where r is the radius of the circle:
Madhava-
A sin³0
3r3 cos³ 0
re
Jyesthadeva
² sine
formula
r cos 0
The bulk of calculus was developed in Europe during the seventeenth century, and it is
on that development that the rest of this chapter is focused.
6 sine
+
5r5 cos
0
Expert Solution
arrow_forward
Step 1: Here
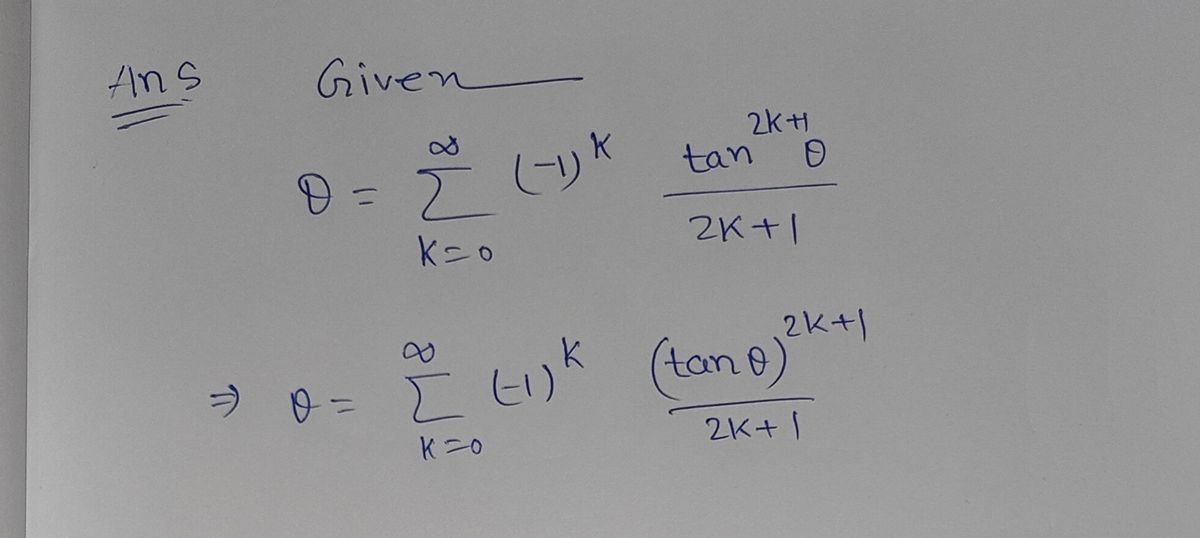
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

