Related questions
Question
Match the answers with questions based on Example 3.10 (I attached pictures of example 3.10 from the textbook)
1.) ball's initial speed
2.) ball's initial speed along the x-component
3.) ball's initial speed along the y-component
4.) ball's initial velocity
5.) ball's acceleration along the y-component
6.) ball's acceleration along the x-component
| A. |
23 m/s, 22° from the horizontal |
| B. |
9.8 m/s2 |
| C. |
-9.8 m/s2 |
| D. |
8.6 m/s |
| E. |
23 m/s |
| F. |
0 |
| G. |
21.3 m/s |
Transcribed Image Text:3.10 A free kick
In a soccer free kick, a player kicks a stationary ball toward the goal that is 18 m away. He kicks the ball at an angle of 22° from the horizontal at a speed of
23 m/s. How long does the ball take to reach the goal? And how far off the ground is the ball when it reaches the goal?
STRATEGIZE This is a projectile motion problem with the initial velocity at an angle above the horizontal. This means that we will have both vertical and
horizontal components of the initial velocity when we apply the equations of Problem-Solving Approach 3.1 O.
PREPARE Following Problem-Solving Approach 3.1 O, we prepare the visual overview shown in Figure 3.31 O. In choosing our axes, we've placed the
origin at the point where the ball is kicked. The initial velocity vector is tilted at 22° above the horizontal, so the components of the initial velocity are
(v.)i= v; cos 0 = (23 m/s)(cos 22°) = 21.3 m/s
(v,);= v; sin 0 = (23 m/s)(sin 22°) = 8.6 m/s
FIGURE 3.31 Visual overview of a kicked soccer ball.
Known
Xi = 9i = 0m, ti= Os
Vi = 23 m/s, 0 = 22°
Xf = 18 m
Xf
Find
X;o Yio ti
Xf> Yfo tf
Transcribed Image Text:Xf
Pina
Xio Yis ti
Xf, Yfs tf
Yos tf
SOLVE The problem-solving approach suggests using one component of the motion to solve for At. We can do so using the kinematic equation for the
horizontal position,
Xf= ¤i + (v,)iAt
We know that x¡ = 0 m, so we can solve this equation for At to get
18 m
At =
0.845 s
21.3 m/s
where we have kept one extra significant figure for our calculations.
We can now use the kinematic equation for the vertical position to find the height of the ball when it reaches the goal:
Yi + (v,);At –¿g(At)²
Om + (8.6 m/s) (0.845 s) – (9.8 m/s³) (0.845 s)² =
Yf
= 3.8 m
The ball is 3.8 m off the ground when it reaches the goal.
ASSESS A height of 3.8 m-about 12 ft-seems reasonable for the height of a kicked ball. Unfortunately, the height of the goal itself is only 2.44 m, so this
kick sails easily over the crossbar.
Expert Solution
arrow_forward
Step 1
The velocity has a magnitude and a direction, the magnitude is called speed.
The horizontal and vertical components of the velocity are shown in figure below.
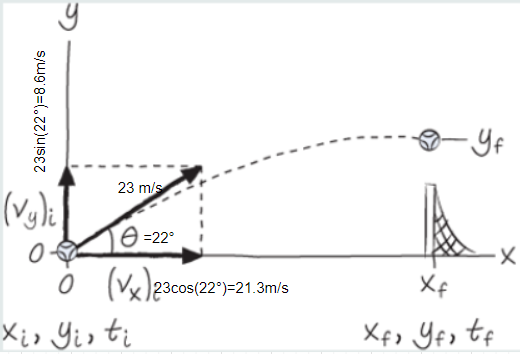
In projectile motion the x and y directions are independent, as gravity acts only vertically the x direction is unaffected, hence in horizontal direction the particle moves with constant velocity whereas vertically it experiences acceleration due to gravitation.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Similar questions
- Help me with that please last 2 parts pleasearrow_forward5. 00 2 Part A The motions described in each of the questions take place at an intersection on a two-lane road with a stop sign in each direction. For each motion; select the correct position versus time graph. For all of the motions, the stop sign is at the position x = x direction.(Figure 1) A driver ignores the stop sign and continues driving east at constant speed. 0, and east is the positive • View Available Hint(s) O A O F Submit Part B Figure K 1 of 1 A driver ignores the stop sign and continues driving west at constant speed. A B ► View Available Hint(s) 14 O A E 14 O F n/myct/itemView?assignmentProblemID=165218943&offset=next 000 000 F4 DD F5 F6arrow_forwardPlease help me. Make sure to give clear answers for all the parts and this problem has 2 parts.arrow_forward
- Use the VELOCITY vs. TIME graph below to answer the following questions. Let west be the positive direction & east be the negative direction. Express all answers in the appropriate mks units. [NOTE: m/s² should be entered as m/s^2.] VELOCITY vs. TIME GRAPH X-velocity (m/s) A.) Over what period of time was the object speeding up? 15 s to 25 s B.) Over what period of time was the object slowing down? 100 Os to 10 s C.) Over what period of time was the object's velocity constant? 50 10 s to 15 s D.) State the magnitude & direction of the object's acceleration at 3 s. west - 50 E.) State the magnitude & direction of the object's acceleration at 13 s. south - 100 F.) State the magnitude & direction of the object's acceleration at 16.5 s. t (s) 25 10 15 20 northarrow_forwardPlease solve I've tried so many waysarrow_forwardNeed help with this practice prob2 Thank youarrow_forward
arrow_back_ios
arrow_forward_ios