
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
PLEASE ANSWER the questions correlty and please answer all the questions with what it regards in saying exactly, please and thank you take your time. Ive read the guide lines and honor code that i can have up to Submit only one question at a time under the appropriate subject. A question can have up to 3 subparts (i.e. part a, b, and c). If you dont belive me here is the link of barthleby saying exactly that thanks: https://bartleby.zendesk.com/hc/en-us/articles/360017462394-How-can-I-ensure-my-questions-get-answered-as-quickly-as-possible-
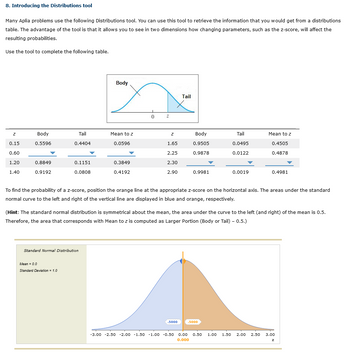
Transcribed Image Text:8. Introducing the Distributions tool
Many Aplia problems use the following Distributions tool. You can use this tool to retrieve the information that you would get from a distributions
table. The advantage of the tool is that it allows you to see in two dimensions how changing parameters, such as the z-score, will affect the
resulting probabilities.
Use the tool to complete the following table.
Z
0.15
0.60
1.20
1.40
Body
0.5596
0.8849
0.9192
Tail
0.4404
0.1151
0.0808
Mean = 0.0
Standard Deviation = 1.0
Body
Standard Normal Distribution
Mean to z
0.0596
0.3849
0.4192
0
Z
Z
1.65
2.25
2.30
2.90
Tail
Body
0.9505
0.9878
.5000
0.9981
Tail
0.0495
0.0122
0.0019
To find the probability of a z-score, position the orange line at the appropriate z-score on the horizontal axis. The areas under the standard
normal curve to the left and right of the vertical line are displayed in blue and orange, respectively.
5000
Mean to z
(Hint: The standard normal distribution is symmetrical about the mean, the area under the curve to the left (and right) of the mean is 0.5.
Therefore, the area that corresponds with Mean to z is computed as Larger Portion (Body or Tail) - 0.5.)
0.4505
0.4878
0.4981
-3.00 -2.50 -2.00 -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 2.00 2.50 3.00
0.000
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- PLEASE ANSWER ALL THE PARTS OF THE QUESTION (THIS IS NOT A GRADED ASSIGNMENT)arrow_forwardPLEASE ANSWER the questions correlty and please answer all the questions with what it regards in saying exactly, please and thank you take your time. Ive read the guide lines and honor code that i can have up to Submit only one question at a time under the appropriate subject. A question can have up to 3 subparts (i.e. part a, b, and c). If you dont belive me here is the link of barthleby saying exactly that thanks: https://bartleby.zendesk.com/hc/en-us/articles/360017462394-How-can-I-ensure-my-questions-get-answered-as-quickly-as-possible-arrow_forwardPlease make sure answers are clear n easy to read. Please do it on white paper. Again make sure the answer is clear.arrow_forward
- i need in words plz no handwritten or no pic However, one of the wrestlers recently pinned Coach Kevin while warming up at a tournament. Kevin forbid the wrestlers to tell the head coach who pinned him. However, from various comments made during practice, the head coach has learned the following facts. Kevin was pinned with an arm bar. Either Gutschow or Woods was at the Reno tournament when Kevin was pinned. If Tyler was at the State tournament when Kevin was pinned, then Colton pinned Kevin. If Colton pinned Kevin, then Kevin was pinned with the banana splits. If Gutschow was at the Reno tournament when Kevin was pinned, then Beachum pinned Kevin. If Tyler was not at the State tournament when Kevin was pinned, then Woods was not at the Reno tournament when Kevin was pinned. If Woods was at the Reno tournament when Kevin was pinned, then Sweig pinned Kevin. Assume that Kevin was pinned with only one wrestling move. Use symbolic logic and valid argument forms to determine who pinned…arrow_forwardQ7- Answer correctly and read the question correctly, If the question is done correctly, I will write a very wonderful and long review about you! Take your time answering the questions, this is all one question, please answer correctly, thank you very much. PLEASE ANSWER ALL of the questions correlty and please answer all the questions with what it regards in saying exactly, please and thank you take your time. Ive read the guide lines and honor code that i can Submit a question at a time under the appropriate subject. A question can have up to subparts (i.e. part a, b, c, ect). If you dont belive me here is the link of barthleby saying exactly that thanks: https://bartleby.zendesk.com/hc/en-us/articles/360017462394-How-can-I-ensure-my-questions-get-answered-as-quickly-as-possible- A large airline company wants to investigate whether the distribution of ticket sales throughout the year differs for domestic versus international destinations. They collect data throughout multiple years…arrow_forwardPLEASE ANSWER the questions correlty and please answer all the questions with what it regards in saying exactly, please and thank you take your time. Ive read the guide lines and honor code that i can have up to Submit only one question at a time under the appropriate subject. A question can have up to 3 subparts (i.e. part a, b, and c). If you dont belive me here is the link of barthleby saying exactly that thanks: https://bartleby.zendesk.com/hc/en-us/articles/360017462394-How-can-I-ensure-my-questions-get-answered-as-quickly-as-possible-arrow_forward
- Please answer the questions correlty and please answer all the questions with what it regards in saying exactly, please and thank you take your time. Ive read the guide lines and honor code that i can have up to Submit only one question at a time under the appropriate subject. A question can have up to 3 subparts (i.e. part a, b, and c). If you dont belive me here is the link of barthleby saying exactly that thanks: https://bartleby.zendesk.com/hc/en-us/articles/360017462394-How-can-I-ensure-my-questions-get-answered-as-quickly-as-possible-arrow_forwardhelp please answer in text form with proper workings and explanation for each and every part and steps with concept and introduction no AI no copy paste remember answer must be in proper format with all workingarrow_forwardIn which order must you complete the proof writing guidelines? Write your proof, create and label an image, restate what is given, plan and organize your reasoning, identify what is given. O Write your proof, create and label an image, restate what is given, plan and organize your reasoning, identify what is given. O Identify what is given, restate what is given, plan and organize your reasoning, write your proof, create and label an image. Ò Identify what is given, create and label an image, restate what is given, plan and organize your reasoning, write your proof. DD F10 000 000 F9 80 F7 F8 F6 F5 F4 F3arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman