
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Geosynchronous satellite moves in a circular orbit around the Earth and completes one circle in the same time T during which the Earth completes one revolution around its own axis. The satellite has mass m and the Earth has mass M and radius R. In order to be geosynchronous, the satellite must be at a certain height h above the Earth’s surface.
a) Derive an expression for h in terms of m, M, R, T and constants.
b) Calculate the numerical value for h in meters.
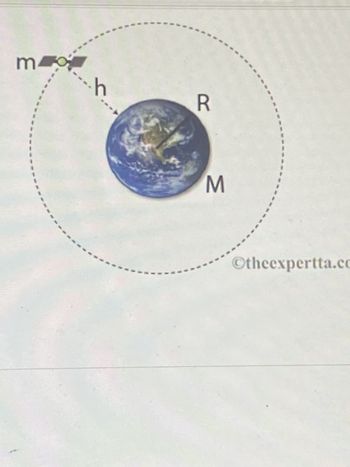
Transcribed Image Text:m
h
R
M
Otheexpertta.co
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Astronomers discover an exoplanet, a planet orbiting a star other than the Sun, that has an orbital period of 3.50 Earth years in a circular orbit around its star, which has a measured mass of 3.80 × 10³0 kg. Determine the radius r of the exoplanet's orbit. r = marrow_forwardA satellite is traveling around a planet in a circular orbit with radius R. It moves in a constant speed of v = 1.1 × 104 m/s. The mass of the planet is M = 6.04 × 1024 kg. The mass of the satellite is m = 1.2 × 103 kg. First, find an expression for the gravitational potential energy PE in terms of G, M, m, and R. a)Calculate the value of PE in joules. b)Enter an expression for the total energy E of the satellite in terms of m and v. c)Calculate the value of the total energy E in joules.arrow_forwardA uniform distribution of dust in the solar system adds to the gravitational attraction of the Sun on a planet an additional forceF = −m C rwhere m is the mass of the planet, C is a constant proportional to the gravitational constant and the density of the dust, and r is the radius vector from the Sun to the planet (both considered as points). This additional force is very small compared to the direct Sun-planet gravitational force.Calculate the period for a circular orbit of radius r0 of the planet in thiscombined field.arrow_forward
- A bead of mass m slides without friction along a curved wire with shape z = f(r) where r = Vr2 + y², i.e. the distance from the z-axis. The wire is rotated around the z-axis at a constant angular velocity w. Gravity acts downward along the z-axis with a constant acceleration g. a) Using Newton's second law in an inertial frame, derive an expression for radius ro of a fixed circular orbit (i.e. a solution with r = ro = const.). What is the normal force the wire applies to the bead to keep it in a circular orbit? b) Show that the equation of motion for r(t) (general equation not the circular motion) is F(1 + f'(r)²) + i² f'(r)f"(r) + gf'(r) – w?r = 0. Using this verify your answer to part (a). c) Consider small displacements from the circular orbit, r = ro+e(t). Derive a condition on the function f(r) such that a circular orbit at r = ro is stable. d) Find the force on the bead in the o direction, i.e. perpendicular to the plane of wire. The angular velocity is w = . Obtain the answer…arrow_forwardAssume a planet is a uniform sphere of radius R that (somehow) has a narrow radial tunnel through its center. Also assume we can position an apple anywhere along the tunnel or outside the sphere. Let Fp be the magnitude of the gravitational force on the apple when it is located at the planet's surface. How far from the surface (what multiple of R) is there a point where the magnitude of the gravitational force on the apple is 0.5 FR if we move the apple (a) away from the planet and (b) into the tunnel? (a) Number: Units: (b) Number: Units:arrow_forwardA geosynchronous Earth satellite is one that has an orbital period of precisely 1 day. Such orbits are useful for communication and weather observation because the satellite remains above the same point on Earth (provided it orbits in the equatorial plane in the same direction as Earth’s rotation). Calculate the radius of such an orbit based on the data for Earth in Appendix D.arrow_forward
- Astronomers discover an exoplanet, a planet orbiting a star other than the Sun, that has an orbital period of 3.17 Earth years in a circular orbit around its star, which has a measured mass of 3.63×1030 kg. Find the radius r of the exoplanet's orbit.arrow_forwardAn exotic planet Vogsphere is known to have a mass that is 1/81 that of the Earth and a radius 0.25 that of the Earth. Astrophysicist Trillian built a rocket and decided to leave the planet and never to return. Given that the escape speed from the Earth is 11.2 km/s, with what speed must Trillian achieve his goal?arrow_forwardAstronomers discover an exoplanet, a planet orbiting a star other than the Sun, that has an orbital period of 3.87 Earth years in a circular orbit around its star, which has a measured mass of 3.77×10^30 kg. Find the radius r of the exoplanet's orbit.arrow_forward
- A 561-kg satellite is in a circular orbit about Earth at a height above Earth equal to Earth's mean radius. (a) Find the satellite's orbital speed. ?m/s (b) Find the period of its revolution. ?h (c) Find the gravitational force acting on it. ? Narrow_forwardThe days on Mars and Earth are of nearly identical length. Earth's mass is 9.35 times Mars's mass, Earth's radius is 1.88 times Mars's radius, and Mars is on average 1.52 times farther away from the Sun than Earth is. The Martian year is 1.88 times longer than Earth's year. Assume that they are both uniform spheres and that their orbits about the Sun are circles. Estimate the ratio (Earth to Mars) of the following. (a) their spin angular momenta(b) their spin kinetic energies(c) their orbital angular momenta(d) their orbital kinetic energiesarrow_forwardAn asteroid is discovered to have a tiny moon that orbits it in a circular path at a distance of 147 km and with a period of 35.0 h. The asteroid is roughly spherical (unusual for such a small body) with a radius of 24.3 km. a) Find the acceleration of gravity at the surface of the asteroid. b) Find the escape velocity from the asteroid.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON