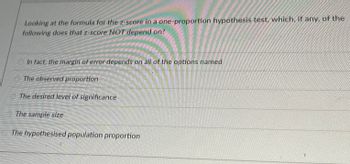
### Understanding the Z-Score in One-Proportion Hypothesis TestsIn the context of hypothesis testing, particularly for a one-proportion test, it is essential to understand which factors influence the z-score calculation. The z-score can be a critical value that helps determine the significance of the observed data. Let's scrutinize an example question that seeks to clarify one aspect of this concept:**Question:**Looking at the formula for the z-score in a one-proportion hypothesis test, which, if any, of the following does that z-score NOT depend on?- \(\circ\) In fact, the margin of error depends on all of the options named- \(\circ\) The observed proportion- \(\circ\) The desired level of significance- \(\circ\) The sample size- \(\circ\) The hypothesised population proportion**Explanation:**- **The Observed Proportion:** The observed proportion is the actual proportion of the sample exhibiting a particular trait. This value directly influences the z-score calculation. - **The Desired Level of Significance (\(\alpha\)):** This represents the threshold at which you reject the null hypothesis. However, note that while the significance level affects decision-making thresholds, it is not a direct component of the z-score calculation itself. - **The Sample Size (\(n\)):** The sample size also plays a critical role in determining the spread and, consequently, the margin of error, which feeds into the z-score. - **The Hypothesised Population Proportion (\(p_0\)):** This is the proportion of the population hypothesized under the null hypothesis and is a fundamental part of the z-score formula.Upon analysis, the z-score itself directly depends on the observed proportion, the hypothesized population proportion, and the sample size. The desired level of significance is crucial for interpreting the z-score but does not impact its calculation.The correct answer here is:- \(\circ\) The desired level of significanceRemember, the significance level affects how you interpret the z-score but does not influence its value directly.

The z-test for one population proportion is a statistical hypothesis test which is used to test the…

Answered: Looking at the formula for the z-score…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

Test whether or not the average salary of males is significantly greater than that of females. The p-value is ________.
The estimated standard error of the mean for a relevant sampling distribution provides an indicator of: The average or standard amount we expect a sample mean to differ from the population mean, if the null hypothesis is true The average or standard amount we expect two study condition means to differ from one another in a repeated measures study design due to chance, if the null hypothesis is true All of these answers are correct The average or standard amount we expect two sample group means to differ from one another in an independent groups study design due to chance, if the null hypothesis is true
Using the chi-square statistics table five working out and answers for these questions
minor mode 5,4,4,4,4,3,3,3,2,2,2,2, 11| 40 8 12 number 11 is 2 and 4 A sample of scores has a mean of M=20,à median of 28, and a mode of 29. What is the most likely shape for the sample distribution
Global Happiness: Everything Up to the Paired-Samples t Test What statistical analysis could be used to determine whether this region has a statistically significantly different mean from the global population mean? z test In which of the following four categories does the situation fall? a. only scale nominals b. nominal independent variables, scale dependent variables c. only nominal variables d. any ordinal variables (that cannot be treated as nominal)
Do men and women select different breakfasts? The breakfasts ordered by randomly selected men and women at a popular breakfast place are shown below. Frequencies of Breakfasts for Men and Women French Toast Pancakes Waffles Omelets Men 81 59 84 87 Women 114 75 104 58 α = 0.05 significance level The test-statistic for this data = (Please show your answer to three decimal places.) The p-value for this sample = (Please show your answer to four decimal places.) Thus, the final conclusion is... There is sufficient evidence to conclude that the distribution of breakfast ordered for men is the same as it is for women. There is insufficient evidence to conclude that the distribution of breakfast ordered for men is not the same as it is for women. There is sufficient evidence to conclude that the distribution of breakfast ordered for men is not the same as it is for women There is sufficient evidence to conclude that breakfast ordered and gender are dependent. There is…
Question Help Use the sample data and confidence level given below to complete parts (a) through (d). A research institute poll asked respondents if they felt vulnerable to identity theft. In the poll, n= 1017 and x = 524 who said "yes." Use a 99% confidence level. Click the icon to view a table of z scores. a) Find the best point estimate of the population proportion p. (Round to three decimal places as needed.) b) Identify the value of the margin of error E. E = (Round to three decimal places as needed.) c) Construct the confidence interval. O
Which of these statements is true? Group of answer choices The p-value is determined by the test statistic and the critical value is determined by the significance level The p-value is determined by the significance level and the critical value is determined by the test statistic.
Sampling distributions of sample means are ______ than distributions of population values. a. Narrower b. Wider c. No different d. More skewed
When testing the difference between two population means under independent sampling, we use the z distribution if _____
Sleeping outlier: A simple random sample of ten college freshmen were asked how many hours of sleep they typically got per night. The results were 24, 8, 6.5, 6, 9, 8.5, 7.5, 6.5, 8.5, 9.5 The data contain an outlier that is clearly a mistake. Eliminate the outlier, then construct a 95% confidence interval for the mean amount of sleep from the remaining values. A 95% confidence interval for the mean amount of sleep from the remaining values is ___ < u < ___.
In a sampling distribution of means, variation is measured using what? OZ score Standard Error O Confidence Intervals O Mean of Means

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS