
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN: 9780133923605
Author: Robert L. Boylestad
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
Please asap
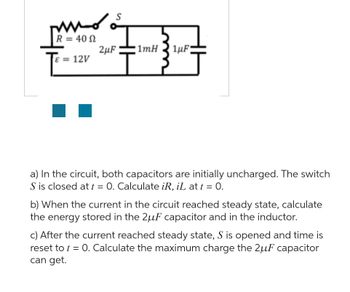
Transcribed Image Text:### Circuit Analysis Problem
#### Circuit Diagram
The given circuit consists of:
- A resistor \( R = 40 \, \Omega \)
- A voltage source \( \epsilon = 12 \, V \)
- Two capacitors with capacitances \( 2 \, \mu F \) and \( 1 \, \mu F \)
- An inductor \( 1 \, mH \)
- A switch \( S \)
The capacitors are initially uncharged, and the switch \( S \) is closed at \( t = 0 \).
#### Problem Statement
a) In the circuit, both capacitors are initially uncharged. The switch \( S \) is closed at \( t = 0 \). Calculate \( i_R \), \( i_L \) at \( t = 0 \).
b) When the current in the circuit reaches steady state, calculate the energy stored in the \( 2 \, \mu F \) capacitor and in the inductor.
c) After the current reached steady state, \( S \) is opened and time is reset to \( t = 0 \). Calculate the maximum charge the \( 2 \mu F \) capacitor can get.
#### Explanation of Diagram:
The provided circuit diagram shows a series-parallel arrangement where:
- The resistor \( R \) and voltage source \( \epsilon \) are in series with the switch \( S \).
- The \( 2 \, \mu F \) capacitor is in parallel with the series combination of the \( 1 \, mH \) inductor and the \(1 \, \mu F \) capacitor.
For the calculations:
1. **At \( t = 0 \):**
- \( i_R \): Current through the resistor immediately after the switch is closed.
- \( i_L \): Current through the inductor immediately after the switch is closed.
2. **At Steady State:**
- Calculate the energy stored in the \( 2 \, \mu F \) capacitor.
- Calculate the energy stored in the inductor.
3. **Reset to \( t = 0 \) after Steady State:**
- Determine the maximum charge that can be stored in the \( 2 \, \mu F \) capacitor when switch \( S \) is reopened and the circuit time is reset to \( t = 0 \).
This diagram and the given
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 10 images

Knowledge Booster
Similar questions
- Which of the following distribution systems would you select for a medical research campus? A) Primary selective system. C) Secondary loop system. B) Distributed radial system. D) Primary and secondary loop system. Authoritative rules for electrical design and installation are contained in which of the following 7) documents? A) ASHRAE Handbook of Fundamentals. B) NFPA 101. C) NEC. The illumination from a point source 4 ft. above a surface is 100 foot-candles, and the surface is normal to the source. What will be the illumination level if the surface is tilted 45°? A) 50 foot-candles. B) 100 foot-candles. C) 71 foot-candles. Which of the following lamp types is generally the most energy efficient? A) Incandescent. C) High intensity discharge. B) LED. D) Fluorescent.arrow_forwardWhat's the general lighting and general-use receptacle demand load for a 24-room motel where each unit is 700 sq ft?arrow_forwardPlease answer ASAP for like this please Asap for like this please... Pleasearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:9781337900348
Author:Stephen L. Herman
Publisher:Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:9780078028229
Author:Charles K Alexander, Matthew Sadiku
Publisher:McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:9780134746968
Author:James W. Nilsson, Susan Riedel
Publisher:PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:9780078028151
Author:Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:Mcgraw-hill Education,