
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
a) List all the odd vertices of the graph.
b) According to Euler’s Theorem, does the graph have an Eulerian circuit? How
do you know?
c) According to Euler’s Theorem, does the graph have an Eulerian path? How
do you know?
What is the difference between a Hamiltonian path and an Eulerian path?
A person starting in Columbus must-visit Great Falls, Odessa, and
Brownsville (although not necessarily in that order), and then return home to
Columbus in one car trip. The road mileage between the cities is shown
|
|
Columbus |
Great Falls |
Odessa |
Brownsville |
|
Columbus |
--- |
102 |
79 |
56 |
|
Great Falls |
102 |
--- |
47 |
69 |
|
Odessa |
79 |
47 |
--- |
72 |
|
Brownsville |
56 |
69 |
72 |
--- |
- Draw a weighted graph that represents this problem in the space below. Use the first letter of the city when labeling each vertex.
- Find the weight (distance) of the Hamiltonian circuit formed using the nearest neighbor algorithm. Give the vertices in the circuit in the order they are visited in the circuit as well as the total weight (distance) of the circuit. Remember to include the unit of measure in your final answer.
.
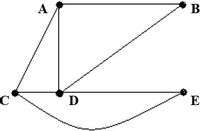
Transcribed Image Text:А
В
D
E
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 1 images

Knowledge Booster
Similar questions
- 1. For each graph in the chart below, fill in each blank of the chart by writing YES or NO in the relevant box. Each graph could have multiple YES or NO answers (and could potentially be all YES or all NO). Note: If a graph has a circuit, then it automatically has a path as well! Graph has an Euler circuit? Graph has an Euler path? Graph has a Hamiltonian circuit? Graph has a Hamiltonian path? 2. Miles Morales is working with Gwen Stacy to uncover the layout of Wilson Fisk's penthouse headquarters. They can see the connected graph in the diagram below, but it is partially covered up with a piece of paper on his desk. Why can they still conclude that it has no Euler path and no Hamiltonian path? Explain. Рaperarrow_forward8 Consider the following graph: b d T/F? The directed graph has an Euler circuit. [(Click to select) The directed graph has an Euler path. [(Click to select) The Euler path is (Click to select) (Click to select) a, d, b, d, e, b, e, c, b, d ΝΑ a, d, b, d, e, b, e, c, a, b a, d, b, d, e, b, e, c, b, a a, b, d, c, e, b, e, c, b, a T/F? (Choose "NA" if there is no Euler path.)arrow_forward4. Given the following directed graph G: a. What is the in-degree of vertex 6? 2 b. What is the out-degree of vertex 4? 3 c. Find a walk of length 5 from vertex 5 to vertex 3. d. Find a path of length 6 from vertex 1 to vertex 2. 4 e. Find a circuit of length 7 starting at vertex 3. 5 7 f. Find a cycle of length 5 starting at vertex 4. g. Is there an edge from vertex 4 to vertex 5 in G2? Why? 6 h. Is there an edge from vertex 4 to vertex 2 in G5? Why?arrow_forward
- Can I get a solution for d~j for this question?arrow_forwardcan you help me fin answer for number 8?arrow_forwardWelcome to Murphman’s Amusement Park! A guest of the park would like to start at the Entrance, walk along each of the midway streets (colored in grey) exactly once, and then leave at the Exit. Note that the railroad tracks are colored purple and are not midway streets. a.Draw a graph in the box above corresponding to this guest’s situation, and determine whether or not the graph has an Eulerian circuit, and if so, give one. If it does not, then explain why not. If the graph does not have an Eulerian circuit, determine whether it has an Eulerian path, and if it does, give one. If it does not, then explain why not. b. Is it possible for the guest to start at the Entrance, walk along all of the midway streets (colored in grey) exactly once, and then leave at the Exit?arrow_forward
- need help with all three questionsarrow_forwardThe symmetric difference graph of two graphs G. (V. E.) and G₂ (V₁ E₂) on the same vertex Set is defined as G₁ AG₂:= (V, E, DE₂). E₁ DE ₂ = (E₁ \ E₂) U (E₂\E.) : E₁ E₂ = €₁ 0 € ₂ If G₁ and 6₂ are euleran, show that every Vertex in G, D G₂ has even degree FACT: Each vertex of a evlenan graph has even degree. SO: Show G₁ D G₂ is eulerian.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

