
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
Let DIST (u, v) denote the distance between vertex u and v. It is well known that distances in graphs satisfy the triangle inequality. That is, for any three vertices u, v, w,
DIST (u, v) ≤ DIST (u, w) + DIST (w, v).
Let D∗ denote the distance between the two farthest nodes in G. Show that for any vertex s
D∗ ≤ 2 max DIST (s, v).
Expert Solution
arrow_forward
Step 1
Given that, DIST(u, v) is the distance between the vertex u and v. If we consider any three vertices u, v, w then DIST (u, v) <= DIST (u, w) + DIST (w, v).
Given that D* is the distance between the two farthest nodes in G.
Consider an example graph G,
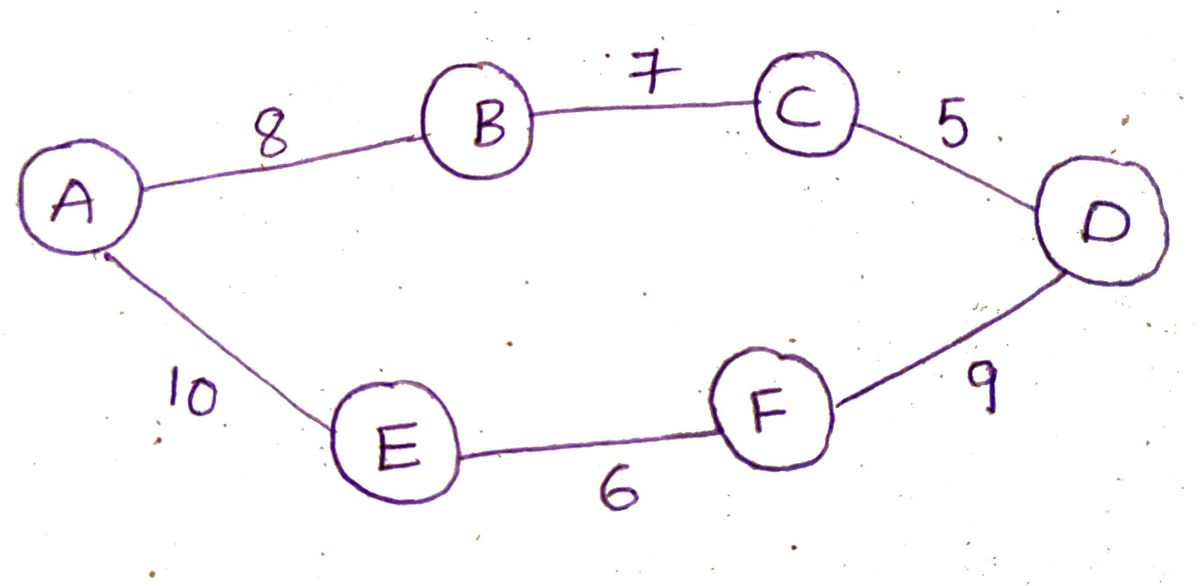
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Assume you have been given a graph with 1 minimum spanning tree and no repeated edge weights. Using the min-cut theorem, prove Boruvka's algorithm is correct. The pseudocode is attached.arrow_forwardlet g be the following dierected grapharrow_forwardLet G be a graph with n vertices. If the maximum size of an independent set in G is k, clearly explain why the minimum size of a vertex cover in G is n - k.arrow_forward
- Consider eight points on the Cartesian two-dimensional x-y plane. a g C For each pair of vertices u and v, the weight of edge uv is the Euclidean (Pythagorean) distance between those two points. For example, dist(a, h) : V4? + 1? = /17 and dist(a, b) = v2? + 0² = 2. Because many pairs of points have identical distances (e.g. dist(h, c) V5), the above diagram has more than one minimum-weight spanning tree. dist(h, b) = dist(h, f) Determine the total number of minimum-weight spanning trees that exist in the above diagram. Clearly justify your answer.arrow_forwardConsider an undirected graph G with 100 nodes. The maximum number of edges to be included in G so that the graph is not connected isarrow_forward1. Run DFS-with-timing on this graph G: give the pre and post number of each vertex. Whenever there is a choice of vertices to explore, always pick the one that is alphabetically first. 2. Draw the meta-graph of G. 3. What is the minimum number of edges you must add to G to make it strongly connected (i.e., it consists of a single connected component after adding these edges)? Give such a set of edges. b.arrow_forward
- Let G be a graph, where each edge has a weight. A spanning tree is a set of edges that connects all the vertices together, so that there exists a path between any pair of vertices in the graph. A minimum-weight spanning tree is a spanning tree whose sum of edge weights is as small as possible. Last week we saw how Kruskal's Algorithm can be applied to any graph to generate a minimum-weight spanning tree. In this question, you will apply Prim's Algorithm on the graph below. You must start with vertex A. H 4 4 1 3 J 2 C 10 4 8 B 9 F 18 8 There are nine edges in the spanning tree produced by Prim's Algorithm, including AB, BC, and IJ. Determine the exact order in which these nine edges are added to form the minimum-weight spanning tree. 3.arrow_forwardGiven a digraph, find a bitonic shortest path from s to every other vertex (if one exists). A path is bitonic if there is an intermediate vertex v suchthat the edges on the path from s to v are strictly increasing and the edges on the pathfrom v to t are strictly decreasing. The path should be simple (no repeated vertices).arrow_forwardLet G = (V, E) be an undirected graph and each edge e ∈ E is associated with a positive weight ℓ(e).For simplicity we assume weights are distinct. Is the following statement true or false? Let T be a minimum spanning tree for the graph with the original weight. Suppose we replace eachedge weight ℓ(e) with ℓ(e)^2, then T is still a minimum spanning tree.arrow_forward
- Consider an undirected graph on 8 vertices, with 12 edges given as shown below: Q2.1 Give the result of running Kruskal's algorithm on this edge sequence (specify the order in which the edges are selected). Q2.2 For the same graph, exhibit a cut that certifies that the edge ry is in the minimum spanning tree. Your answer should be in the form E(S, V/S) for some vertex set S. Specifically, you should find S.arrow_forwardConstruct all regular graphs that exist for the vertex set V = {1, 2, 3, 4}. For example, G = (V,E0) where E0 = {} is one possible grapharrow_forwardWrite a function that returns true (1) if there is an edge between two vertices u and v in an adjacency-listed directed graph.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education