
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:Let \( V = \mathbb{R}^3 \) and define vector addition as \((x, y, z) + (x', y', z') = (x + x', y + y', z + z')\) (standard addition) and scalar multiplication as \(k(x, y, z) = (kx, ky, 2z)\) (not the standard scalar multiplication). Determine if \( V \) is a vector space.
Expert Solution
arrow_forward
Step 1
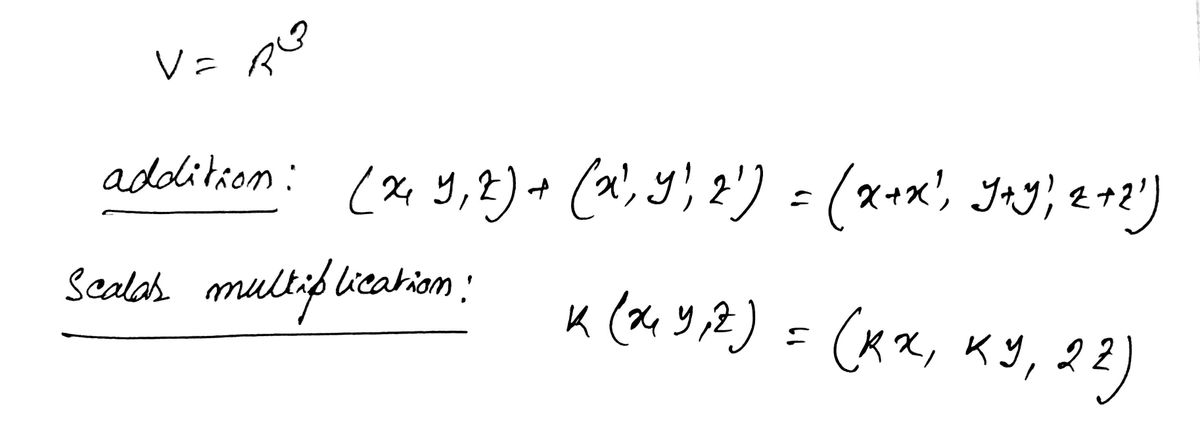
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Consider the vectors u₁ = [1,0,−1], _U2 = [1,0,0] and u3 = [0, 1, 1], v = [5, 1, 3] and w = = [1,0,3]. (a) Show that the vectors u₁, u₂ and u3 are linearly independent. (b) Show that the vector v is in the span of u₁, U₂ and u3. (c) Find the coordinate vector of v with respect to {U₁, U2, U3}. (d) Write the zero vector as as a non-trivial linear combination of the vectors u₁, U2, U3 and w.arrow_forwardCompute the curl of each of the following vectors: V = (yz, xz, xy) F = (x, y, z) = = ( Note: Y 2 (x² + y² +2²)³/²¹ (x² + y² + x2)³/²¹ (x² + y² + x2)³/2 • If the answer is a scalar, you can just type it in the box (using the Calcpad if you like, or using / for fractions, ^ for exponents, etc.) For multiplication, you can either leave a space, or use *. So x*x=xx = x². Note that this is not the same as xx without a space; that will get read as an entirely different variable! • If you need to enter a vector, enter an ordered list of components, so for A you can enter either A = (A₂, Ay, A₂) = {Ax, Ay, Az} . Note that the system isn't great with multiplying through by overall factors, so it's better not to write e.g. • If you need to enter O, enter it in three components, as (0, 0, 0) or {0,0,0}. V x V = ▼ xr= vx= (2A, 2A, 2A₂).arrow_forward2a)Use triple scalar to verify that the following vectors are not coplanar. ā=[-2,1,0], b=[-3,4,5], c =[2,0,3] b) Write a = [-4,1,7] as a linear combination of a,b,carrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

