
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
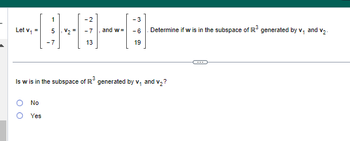
Transcribed Image Text:Let v₁ =
O
1
5
-7
No
Yes
V₂ =
-2
-7
13
and w=
- 3
-6
19
Is w is in the subspace of R³ generated by v₁ and v₂?
Determine if w is in the subspace of R³ generated by v₁ and v₂.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- W is a subspace of R4 consisting of vectors of the form. Determine dim(W) when the components of x satisfy the given conditions.arrow_forwardLet W be the subspace spanned by u₁ and u₂, and write y as the sum of a vector in W and a vector orthogonal to W. -0- y = -2 3,4₁ 5 The sum is y = y + z, where y= (Simplify your answers.) -3 -1 is in W and Z= is orthogonal to W.arrow_forwarda b 6. Let H be a subspace of M2x2 whose vectors are of the form Then, B с 0 is a basis for H. 10 Find the coordinate vector of v = according to the basis, B.arrow_forward
- 1 2 7 Let v, = and w = - 1 3 8 2 a. Is w in {v1, V2, V3}? How many vectors are in {v1, V2. V3}? b. How many vectors are in Span{v1, V2, V3}? c. Is w in the subspace spanned by {v1, V2, V3}? Why? a. Is w in {v1, V2. V3}? O A. Vector w is not in {v1, v2, V3} because it is not v1, V2, or v3. O B. Vector w is in {v1, v2, V3} because it is a linear combination of v,, v2, and v3. O C. Vector w is not in {v1, v2, V3} because it is not a linear combination of v1, V2, and v3. O D. Vector w is in {v1, V2, V3} because the subspace generated by v1, V2, and v3 is R°. How many vectors are in {v1, v2, V3}? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The number of vectors in {v1, V2, V3} is O B. There are infinitely many vectors in {v1, V2, V3).arrow_forwardU₁ = 4 #0-0 -2,1₂ = and и3 = -32 Note that u₁, ₂ and 3 are orthogonal. V = Given v = 4 -0₁ 2 find the coordinates for v in the subspace Wspanned by 4 4 4 U₁ + -8 -8 U₂ +1 U3|arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

