
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Let V be a vector space over R, and let S1 and S2 be subspaces of V.
a) Prove that S1 ⊆ S2 ⇒ dim(S1) ≤ dim(S2).
b) Prove that (S1 ⊆ S2 and dim(S1) = dim(S2)) ⇒ S1 = S2
c) Prove that if u1, . . . , uk are linearly independent
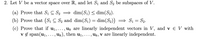
Transcribed Image Text:2. Let V be a vector space over R, and let S1 and S2 be subspaces of V.
(a) Prove that Si C S2 = dim(S1) < dim(S2).
(b) Prove that (Sı C S2 and dim(S1) = dim(S2)) = S1 = S2.
(c) Prove that if u1,..., uk are linearly independent vectors in V, and v e V with
v 4 span(u1,
Ug are linearly independent vectors in V, and v e V with
U%), then u1,... , Uk, v are linearly independent.
•.
u
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Let V be the vector space of polynomials in t of degree ≤ 3. Determine whether thefollowing vectors ⃗u, ⃗v, ⃗w are linear independent or dependent ?⃗u = t3 − 3t2 + 5t + 1, ⃗v = t3 − t2 + 8t + 2, ⃗w = 2t3 + 4t2 + 9t + 5arrow_forwardConsider the following vectors in R³: V1 = W₁ = V2 = 5 2 W2 = 2 -5 2 W3 = Let V be the subspace spanned by {w₁, W2, W3}. Find a linearly independent set of vectors {v₁, v₂} that spans V, so that neither v₁ nor v₂ is a scalar multiple of any of W1, W2, W3. 19arrow_forwardLet {w1, w2, ..., Wk} be a basis for a subspace W of the vector space V. Let v be a vector in W1. Show that 1 (v, w1) + 2 (v, w2) + 3 (v, w3) + ...+ k (v, wk) cannot be a negative number.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

