Let the transfer function H(s) of an excitable neuron be given by: s+ B H(s) = output input Y (s + x) ³. a) Using partial fraction decomposition, write H(s) as the sum of two partial fractions, i.e., solve for A and B in this equation in terms of a and B: A B H(s) = Y(s + a)² + (s + a)³ b) Write the time-domain impulse response h(t) for the neuron. Please consult a table of Laplace transforms, or use this relationship: L{teat} = n! (s-a)n+1 c) Using the expression derived in part (b) and the code provided, plot in Matlab the response of the neuron to an impulse Vimpo(t), where Vimp = 150 mV. You will need to modify the code to include an anonymous function that defines your h(t). Use the constants provided in the code, gamma = y = 500 s¹, beta = ß = 0.1 s´¹, and alpha =α= 104 s¹. Assume the baseline membrane potential is Vbas = -70 mV, and h(t) represents a positive change above Vbas. What is the maximum value of the membrane potential (or change above Vbas) in the single impulse response? d) Now assume the input is an impulse train, or a sequence of impulses separated by a fixed delay T. The same code provided will also plot the response of the neuron to a sequence of Vimp [8(t) + 8(t − T) + 8(t − 2T) + ··· ], for up to 15 impulses, using four different values of T: 1.00 ms, 0.30 ms, 0.10 ms, and 0.05 ms. The neuron will activate when its membrane potential becomes more positive than its activation threshold Vthr = -50 mV. Which excitation signals (i.e., which values of T) lead to neuron activation? What is the time delay between the start of the impulse train (t = 0) and the activation of the neuron?
Let the transfer function H(s) of an excitable neuron be given by: s+ B H(s) = output input Y (s + x) ³. a) Using partial fraction decomposition, write H(s) as the sum of two partial fractions, i.e., solve for A and B in this equation in terms of a and B: A B H(s) = Y(s + a)² + (s + a)³ b) Write the time-domain impulse response h(t) for the neuron. Please consult a table of Laplace transforms, or use this relationship: L{teat} = n! (s-a)n+1 c) Using the expression derived in part (b) and the code provided, plot in Matlab the response of the neuron to an impulse Vimpo(t), where Vimp = 150 mV. You will need to modify the code to include an anonymous function that defines your h(t). Use the constants provided in the code, gamma = y = 500 s¹, beta = ß = 0.1 s´¹, and alpha =α= 104 s¹. Assume the baseline membrane potential is Vbas = -70 mV, and h(t) represents a positive change above Vbas. What is the maximum value of the membrane potential (or change above Vbas) in the single impulse response? d) Now assume the input is an impulse train, or a sequence of impulses separated by a fixed delay T. The same code provided will also plot the response of the neuron to a sequence of Vimp [8(t) + 8(t − T) + 8(t − 2T) + ··· ], for up to 15 impulses, using four different values of T: 1.00 ms, 0.30 ms, 0.10 ms, and 0.05 ms. The neuron will activate when its membrane potential becomes more positive than its activation threshold Vthr = -50 mV. Which excitation signals (i.e., which values of T) lead to neuron activation? What is the time delay between the start of the impulse train (t = 0) and the activation of the neuron?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Replace H(s) with the second picture, only need help with part a and b please
![Let the transfer function H(s) of an excitable neuron be given by:
s+ B
H(s) =
output
input
(s + a)³
Y
a) Using partial fraction decomposition, write H(s) as the sum of two partial fractions, i.e.,
solve for A and B in this equation in terms of a and ß:
A
B
H(S) = Y | S
(s + a)²
(s+ a)³.
b) Write the time-domain impulse response h(t) for the neuron. Please consult a table of
Laplace transforms, or use this relationship:
L{teat} =
+
n!
(s-a)n+1
c) Using the expression derived in part (b) and the code provided, plot in Matlab the
response of the neuron to an impulse Vimpo(t), where Vimp = 150 mV. You will need to
modify the code to include an anonymous function that defines your h(t). Use the
constants provided in the code, gamma ⇒ y = 500 s¹¹, beta = ß = 0.1 s¹¹, and alpha = a =
104 s¹. Assume the baseline membrane potential is Vbas = -70 mV, and h(t) represents a
positive change above Vbas. What is the maximum value of the membrane potential (or
change above Vbas) in the single impulse response?
d) Now assume the input is an impulse train, or a sequence of impulses separated by a fixed
delay T. The same code provided will also plot the response of the neuron to a sequence
of Vimp [8(t) + 8(t − T) + 8(t − 2T) +...], for up to 15 impulses, using four different
values of T: 1.00 ms, 0.30 ms, 0.10 ms, and 0.05 ms. The neuron will activate when its
membrane potential becomes more positive than its activation threshold Vthr = -50 mV.
Which excitation signals (i.e., which values of T) lead to neuron activation? What is the
time delay between the start of the impulse train (t = 0) and the activation of the neuron?](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ff615326e-a737-4ff6-ab97-e2ce7686d995%2Fe8519ce5-afe5-4319-a1c1-ca5260203944%2Fyxj8v7h_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Let the transfer function H(s) of an excitable neuron be given by:
s+ B
H(s) =
output
input
(s + a)³
Y
a) Using partial fraction decomposition, write H(s) as the sum of two partial fractions, i.e.,
solve for A and B in this equation in terms of a and ß:
A
B
H(S) = Y | S
(s + a)²
(s+ a)³.
b) Write the time-domain impulse response h(t) for the neuron. Please consult a table of
Laplace transforms, or use this relationship:
L{teat} =
+
n!
(s-a)n+1
c) Using the expression derived in part (b) and the code provided, plot in Matlab the
response of the neuron to an impulse Vimpo(t), where Vimp = 150 mV. You will need to
modify the code to include an anonymous function that defines your h(t). Use the
constants provided in the code, gamma ⇒ y = 500 s¹¹, beta = ß = 0.1 s¹¹, and alpha = a =
104 s¹. Assume the baseline membrane potential is Vbas = -70 mV, and h(t) represents a
positive change above Vbas. What is the maximum value of the membrane potential (or
change above Vbas) in the single impulse response?
d) Now assume the input is an impulse train, or a sequence of impulses separated by a fixed
delay T. The same code provided will also plot the response of the neuron to a sequence
of Vimp [8(t) + 8(t − T) + 8(t − 2T) +...], for up to 15 impulses, using four different
values of T: 1.00 ms, 0.30 ms, 0.10 ms, and 0.05 ms. The neuron will activate when its
membrane potential becomes more positive than its activation threshold Vthr = -50 mV.
Which excitation signals (i.e., which values of T) lead to neuron activation? What is the
time delay between the start of the impulse train (t = 0) and the activation of the neuron?
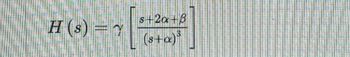
Transcribed Image Text:H(s) = Y
P
s+2a+8
(s+a)³
Expert Solution
Step 1
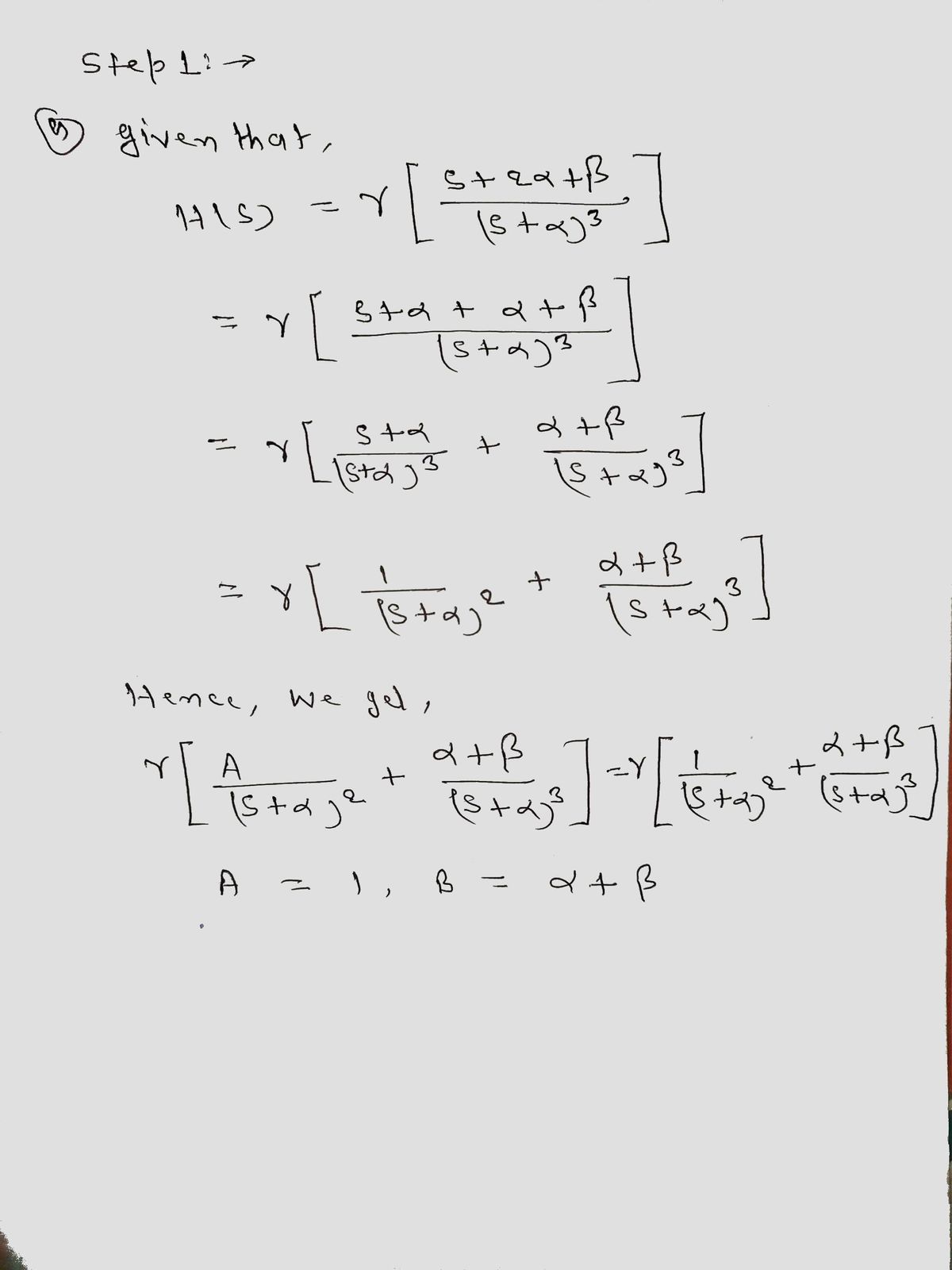
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
