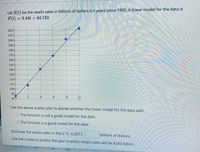
Let S(t) be the retails sales in billions of dollars in t years since 1995. A linear model for the data is F(t) = 9.44t + 84.182. 220- 210- 200- 190- 180- 170 160 150 140 130 120 110- 100- 90 3. 9 12 804 Use the above scatter plot to decide whether the linear model fits the data well. O The function is not a good model for the data O The function is a good model for the data. Estimate the retails sales in the U. S. in 2017. billions of dollars. Use the model to predict the year in which retails sales will be $243 billion.

How much should a healthy Shetland pony weigh? Let x be the age of the pony (in months), and let y be the average weight of the pony (in kilograms). x 3 6 12 20 26 y 60 95 140 160 189 (a) Make a scatter diagram of the data and visualize the line you think best fits the data.   Flash Player version 10 or higher is required for this question. You can get Flash Player free from Adobe's website.   (b) Would you say the correlation is low, moderate, or strong?  low moderate     strong Would you say the correlation is positive or negative?  positive negative     (c) Use a calculator to verify that          x = 67,           x2 = 1265,           y = 644,           y2 = 93,546,  and          xy = 10,544.  Compute r. (Round your answer to three decimal places.)  As x increases from 3 to 26 months, does the value of r imply that y should tend to increase or decrease? Explain your answer.  Given our value of r, y should…

800 700 600 500 400 300 200 100 1 2345 67 8 9 10 11 12 13 14 15 16 age Its slope is positive. It passes through the point (0,0). It stops at y = 800. None of the answers is correct.

This graph displays the distance traveled by a golf cart as a function of time in seconds. C D Time (seconds) B E At which time interval is the golf cart moving fastest? A between A and B B. between B and C C. between C and D D. between D and E Distance Traveled

Marine scientists use a linear model for the speed c of sound in the oceans as a function of the salinity S at a fixed depth and temperature.† In the following table, one scientist recorded data for c and S at a depth of 500 meters and a temperature of 15 degrees Celsius. Here c is measured in meters per second and S in parts per thousand. Salinity S Sound speed c 35.0 1515.36 35.6 1516.08 36.2 1516.80 36.8 1517.62 37.4 1518.24 (a) Looking over the table, the scientist realizes that one of the entries for sound speed is in error. Which entry is it?S = What is the correct speed?c =  m/sec(b) Explain in practical terms the meaning of the slope of the linear model for c in terms of S at the given depth and temperature. The slope means that, at the given depth and temperature, for an increase in salinity of  part per thousand the speed of sound increases by  meters per second. (c) Calculate c(38.2).c(38.2) =  m/secExplain in practical terms what it means. This means…