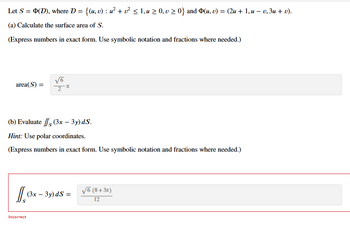
Let S = Þ(D), where D = {(u, v) : u² + v² ≤ 1, u ≥ 0, v ≥ 0} and Þ(u, v) = (2u + 1, u − v, 3u + v). (a) Calculate the surface area of S. (Express numbers in exact form. Use symbolic notation and fractions where needed.) area(S) = √6 27 (b) Evaluate (3x − 3y) dS. Hint: Use polar coordinates.

Help find the areas of the rectangles in image attached

A gift box is made in the shape of a triangular prism. The triangular end is an equilateral triangle with length x cm and the length of the box is The volume of the box is 300 cm³. r cmX Кx ст у ст х ст (a) Find an expression for y in terms of x. (b) Show that the total surface area A cm?, of the box, is given by 1200v3, v3x? 2 A = (c) Find the value of x that gives the minimum total surface area. Justify your answer.