
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Transcribed Image Text:e Edit View History Bookmarks Profiles Tab Window Help
en HW 4
fiu.instructure.com
work 4 (Fall 21).pdf
30%
F2
X
#3
#
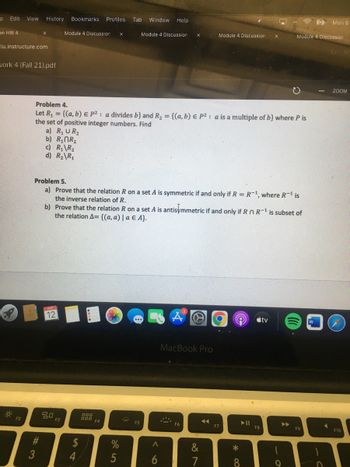
Problem 4.
Let R₁ = {(a, b) E P²: a divides b} and R₂ = {(a, b) E P²: a is a multiple of b} where P is
the set of positive integer numbers. Find
a) R₁ UR₂
b) R₁NR₂
c) R₁ R₂
d) R₂\R₁
Module 4 Discussion X
SEP
12
Problem 5.
a) Prove that the relation R on a set A is symmetric if and only if R = R-¹, where R-¹ is
the inverse relation of R.
b) Prove that the relation R on a set A is antisymmetric if and only if R n R-¹ is subset of
the relation A= {(a, a) | a € A}.
20
F3
$
4
000
DOO
F4
%
5
Module 4 Discussion X
S
F5
^
6
MacBook Pro
F6
87
&
Module 4 Discussion X
◄◄
F7
*
8
► 11
F8
tv
Module 4 Discussion
►►
9
(
F9
2 Mon 8:
W
1
U
ZOOM
F10
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Let A= -4 1 -3 3 8 0 5 a) A-BT and B= = b) -3B12 +2 A32 c) B₁* A*2 -2 3 -1 -1 4] -2 10 7 · Calculate the following:arrow_forwardWhat is the value of x? * 23 16 A) 37.7 C) 6.8 B) 31.2 D) 42.7arrow_forwardI al 联系。 (c) (d) that Write down 505 as a sum of two squares. Write down 197 as the sum of four squares. Find all positive primitive Pythagorean triples (x, y, z), with y even, such x+y+z= 30.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

