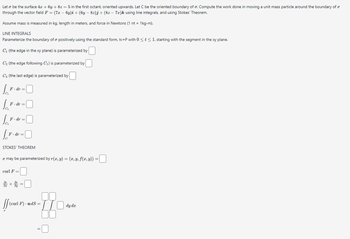
Let o be the surface 4x + 6y + 8z = 5 in the first octant, oriented upwards. Let C be the oriented boundary of o. Compute the work done in moving a unit mass particle around the boundary of o through the vector field F = (7x - 6y)i + (6y − 8z)j + (8z – 7x)k using line integrals, and using Stokes' Theorem. Assume mass is measured in kg, length in meters, and force in Newtons (1 nt = 1kg-m). LINE INTEGRALS Parameterize the boundary of o positively using the standard form, tv+P with 0 ≤ t≤ 1, starting with the segment in the xy plane. C₁ (the edge in the xy plane) is parameterized by C₂ (the edge following C₁) is parameterized by C3 (the last edge) is parameterized by Sai F. dr = Ja F.dr = Je₂ F.dr = fo F.dr = STOKES' THEOREM o may be parameterized by r(x, y) = (x, y, f(x, y)) = | curl F = ox ff (c (curl F) · ndS= TIO dydz

Compute the flux of the vector field = zi + 4y3 through the cylindrical surface shown below, if a = 2 and b = 2 and it is oriented away from the z-axis. flux = a

Let v = (x³ cos z, 1 - 3x²y cos z − 3yz² sinx, z³ sin x) be the velocity field of a fluid. Compute the flux of v across the surface x² + y + z² = 25 where y> 0 and the surface is oriented away from the origin. Note that this surface is not closed.

A particle moves along line segments from the origin to the points (3, 0, 0), (3, 3, 1), (0, 3, 1), and back to the origin under the influence of the force field F(x, у, 2) z2i + 3xyj + 4y?k. Use Stokes' Theorem to find the work done. F• dr = 129/2

In order to verify Stokes' theorem for the vector field F = 3xyi - 2zyk permeating a square coil placed in the xy plane and extending from 0 to 1 in both Cartesian directions, first calculate the line integral of F around the coil, and then evaluate the corresponding flux of V x F across the surface enclosed by the coil.