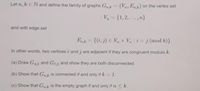
Let n, k EN and define the family of graphs G, (V, Ek) on the vertex set V,= (1,2,... ,n} and with edge set Enk= {(i,j) E V, x V: ij (mod k)}. In other words, two vertices i and j are adjacent if they are congruent modulok. (a) Draw G12 and G73 and show they are both disconnected. (b) Show that G is connected if and only if k 1. (c) Show that Gk is the empty graph if and only if n

5.) Determine if each of the given pairs of graphs are Isomorphic If they are provide an isomorphism; if they are not, find the a) b) invariant that no meet. el G es ea 9 S Z Ca €3 ^* e4 H (4 9 C3 X t u

Draw a Cayley graph for Z/7Z with generating set {2¯,5¯}.

Prove: “The complement of the graph G is an Eulerian graph whenever G is also an Eulerian graph of odd order and the complement of G is connected.” Give afigure and details to validate the proof.